Урок № 1

Тема. Вступление. Точка и прямая. Свойства точек и прямых

Цель: ознакомить учащихся с предметом изучения геометрии, планиметрии и с понятием простейших фигур в геометрии, добиваться от учащихся сознательного усвоения терминологии, описывает взаимное расположение точек и прямых на плоскости, формулирование основных свойства расположения точек и прямых; выработать первичные умения обозначать точки и прямые на рисунке, описывать ситуацию, изображенную на рисунке и, наоборот, по описанию ситуации выполнять соответствующие рисунки, пользуясь самым простым чертежным прибором.

Тип урока: усвоение знаний, умений и навыков.

Форма проведения: беседа.

Наглядность и оборудование: демонстрационные чертежные инструменты.

ХОД УРОКА

И. Организационный момент

Учитель сообщает учащихся об организации учебного процесса по изучению геометрии, знакомит с требованиями программы по знаний и умений (в адаптированной форме), объясняет структуру учебника, его особенности.

II. Формулировка цели и задач урока

Исходя из темы урока и согласование ее с учениками, учитель формулирует основную дидактическую цель урока (см. выше).

III. Усвоение новых знаний

План изучение нового материала

1°. Вступительная беседа.

а) Зарождение геометрии;

б) геометрия Евклида;

в) с истории развития геометрии, строение геометрии;

г) простейшие геометрические фигуры;

д) что такое аксиома.

2°. Точка i прямая.

3°. Свойства точек и прямых.

а) Свойство принадлежности точек и прямых;

б) аксиома проведение прямой;

в) аксиома размещение точек на прямой.

Методический комментарий

1°. Дополнительный материал для вступительной беседы о развитии геометрии можно взять из книг: Глейзер Г. Ы. История математики в школе.- М.: Просвещение, 1982, 1983; Большая советская энциклопедия.- М.: Советская энциклопедия, 1971.- Т. 6.- С. 307.

Во вступительной беседе можно использовать геометрические знания, которые учащиеся приобрели в 1-6 классах, и обратиться к их жизненного опыта.

2°. Во время изложение этого вопроса следует напомнить учащимся, как изображается прямая и точки, их обозначения (следует указать на то, что для различения теперь обычно прямую будем обозначать одной маленькой латинской буквой, а точки - большими латинскими буквами).

3°. Новые термины «лежит», «не положено», «проходит через точку», «пересекаются», «лежит между» и т.п., следует вводить одновременно с выполнением рисунка.

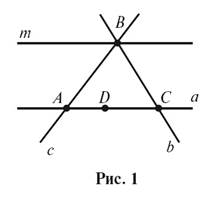
При этом, введя понятия, учитель формулирует аксиому проведения прямой и аксиому размещение точек на прямой. Во время объяснения можно использовать рисунок 1.

IV. Первичное осознание новых знаний

Для усвоение введенной терминологии и аксиом можно выполнить устные упражнения.

Выполнение устных упражнений

1. На прямой AB обозначено точку C. лежит Ли точка A на прямой BC? Лежит ли точка B на прямой AC?

2. Точка A лежит на прямой c, а точка B не лежит на прямой c. Пересекаются ли прямые c и AB? Если да, то назовите точку их пересечения.

3. Через точку A проведены две прямые. Могут ли эти прямые иметь общую точку B, отличную от точки A?

4. Точка B лежит на прямой между точками A и C. Как размещены точки B и C относительно точки A?

5. На прямой отмечены точки K, L, M, N (рис. 2).

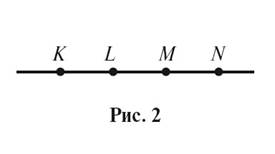
Назовите:

а) точку, что лежит между точками L i N;

б) точки, что лежат между точками K и N;

в) две точки, лежащие по одну сторону от точки L;

г) точку, по разные стороны от которой лежат точки K i M.

6. Рассмотрите рисунок 1 и ответьте на вопрос.

а) На которых прямых лежит точка A? точка B? точка C? точка D?

б) прямые проходят через точки: A; B; C; D?

в) В которой точке пересекаются прямые a и b; b и c; c i m; b i m?

г) В которой точке пересекаются три прямые? Назовите эти прямые.

д) точка на рисунке лежит между двумя другими? Можно сказать, что точка A лежит между точками B и D?

Выполнение графических упражнений

Проведите прямую.

а) Отметьте точки A и B,лежащие на этой прямой, и точки C и D не лежат на ней. Как можно назвать эту прямую?

б) Проведите еще одну прямую через точки A и C. Сколько общих точек имеют построены прямые?

Выполнение письменных упражнений

Уровень А

1. Отметьте точки B и C. Проведите через них прямую. Проведите еще одну прямую так, чтобы она проходила через точку B, но не проходила через точку C. Сколько общих точек имеют эти прямые?

2. На прямой точки E и F лежат по разные стороны от точки D. Как размещены точки D и F относительно точки E? Может ли точка F лежать между точками D и E?

Уровень Б

1. Дано четыре точки, причем никакие три из них не лежат на одной прямой. Через каждые две из данных точек проведена прямая. Сколько всего прямых проведено?

2. На прямой точка B лежит между точками A и C. Отметьте на этой прямой точку D,лежащую между точками B и C. Назовите точку, которая лежит между точками A и D. Какие из обозначенных точек лежат по одну сторону от точки C?

Уровень В

Сколько прямых могут определить четыре точки? Рассмотрите все возможные случаи. Сделайте рисунки.

Методический комментарий

Необходимо с первых уроков во время решения упражнений разного уровня сложности приучать учащихся к предыдущему осуществления определенных последовательных рассуждений, основанных на содержании рассматриваемых понятий и на аксиомах.

Например

Отметьте точки B и C. Проведите через них прямую. Проведите еще одну прямую так, чтобы она проходила через точку B, но не проходила через точку C. Сколько общих точек имеют эти прямые?

Решения. Обозначим точки B и C. За аксиомой проведения прямой, через эти две точки можно провести прямую и только одну (рис. 3).

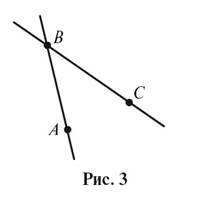
Возьмем точка A не лежит на прямой BC. Тогда через точки A и B, по аксиомой проведение прямой, можно провести прямую AB, до того только одну.

Следовательно, прямые AB i BC имеют одну общую точку B.

V. Итоги урока

Диктант

1. Проведите прямую, использовав аксиому проведения прямой, отметьте ее.

2. Проведите прямую a, отметьте точку C, которая лежит на прямой a точку D, не лежащую на прямой a. Проведите прямую b,проходящую через точку D и пересекает прямую a. Обозначьте точку пересечения прямых буквой F.

3. Отметьте на прямой a точки M, S i K так, чтобы точка K лежала между точками M и S. Отметьте на прямой точку A, чтобы точки S i K лежали по одну сторону, а точка M - по другую сторону от точки A. Прочитайте названия точек по порядку, начиная с точки M. Запишите образованное слово.

VI. Домашнее задача

1. Отметьте две точки и от руки проведите через них прямую. Проверьте правильность построения с помощью линейки. Какой аксиомой вы воспользовались?

2. Точки M i N лежат на прямой по одну сторону от точки K. из этих трех точек не может лежать между двумя другими? Ответ обоснуйте.

3. Точки A, B, C лежат на одной прямой, а точка D не лежит на этой прямой. Через каждые две из данных точек проведена прямая. Сколько всего прямых проведено?

4. На прямой обозначены точки X ,Y, Z, причем точки X и Y лежат по одну сторону от точки Z, а точки X и Z-по одну сторону от точки Y . Какая из трех точек лежит между двумя другими?

Дополнительная задача

Сколько различных прямых могут задавать точки:

а) A, B, C;

б) A, B, C, D;

в) A, B, C, D, O?

Ответ поясните, проиллюстрировав ее рисунками.

Источники:

1. Уроки геометрии. 7 класс./ С. П. Бабенко - Х.: Изд. группа «Основа», 2007.- 208 с.