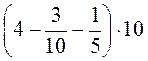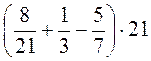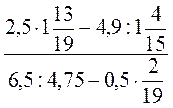Урок № 1
Тема. Преобразования выражений. Повторение и систематизация материала 5-6 классов
Цель: систематизировать и обобщить знания учащихся о преобразовании выражений, полученные в 5-6 классах.
Тип урока: повторение и систематизация знаний.
Ход урока
I. Организационный момент
Вступительная беседа.
II. Актуализация опорных знаний
На эту тему отводится два урока.
@ Тождественные преобразования выражений является одним из важнейших разделов школьной алгебры.
С простейшими преобразованиями выражений учащиеся знакомятся уже в курсе математики 5-6 классов, где рассматриваются возведения подобных слагаемых, вынесение общего множителя за скобки; раскрытие скобок, перед которыми стоит знак «+» или «-». Но поскольку более подробно тема «Выражения с переменными» будет изучаться позже, на этих уроках мы акцентируем внимание на повторении основных способов действий при преобразовании выражений и вычислении значений числовых выражений в том объеме, что является необходимым для изучения следующей темы «Линейное уравнение с одной переменной».
Поэтому на первом уроке мы рассматриваем вопрос «Свойства действий над числами», а на следующем - «Преобразование выражений». На уроке, посвященном теме «Свойства действий над числами», желательно рассмотреть следующие вопросы:
1. Алгоритмы выполнения действий с натуральными и рациональными числами.
2. Свойства арифметических действий над числами.
3. Рационализация вычислений с использованием свойств действий над числами.
Работу желательно организовать так, чтобы ученики не просто выполнили определенные задачи, а чтобы осознали алгоритмы и способ их применения, а также свойства арифметических действий и удостоверились в преимуществах их применения для упрощения вычислений.
Следует заметить, что надо выделить время еще на один вид работы, очень важной для восприятия материала о преобразовании выражений, - чтение и запись числовых выражений.
 Кроме того, не будет лишним напомнить учащимся о видах чисел, которые они изучили в 5 и 6 классах, ибо умение классифицировать математические объекты являются необходимым условием осознанного использования соответствующих алгоритмов. Для упрощения работы учащихся с теоретическим материалом предлагаем конспект 1 (или для фронтальной работы, или в виде раздаточного материала на каждую парту).
Кроме того, не будет лишним напомнить учащимся о видах чисел, которые они изучили в 5 и 6 классах, ибо умение классифицировать математические объекты являются необходимым условием осознанного использования соответствующих алгоритмов. Для упрощения работы учащихся с теоретическим материалом предлагаем конспект 1 (или для фронтальной работы, или в виде раздаточного материала на каждую парту).
|
Конспект 1 |
1. |
Рациональные числа |
|
|
|
↓ |
↓ |
|
|
цели |
дробные |
|
|
↓ |
|
|
натуральные |
|
2. Как выполняется: а) сложение; б) вычитание; в) умножение; г) деление рациональных чисел?
Объясните, рассмотрев примеры: |
1) |
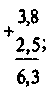
|
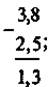
|
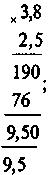
|
3,8 : 2,5 = 38 : 25 = 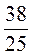 = = 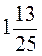 . . |
2) -3,8 - 2,5 = - (3,8 + 2,5) = -6,3;
-3,8 + 2,5 = - (3,8 - 2,5) = -1,3;
-3,8 · (-2,5) = 9,5;
-3,8 : 2,5 = - (3,8 : 2,5) = -1,52. |
3. Свойства арифметических действий: |
|
а) Переставная:
а + b = b + а - добавление,
ab - ba - умножение;
б) связующее:
а + (b + с) = (a + b) + с - сложение,
а(bс) = (ab) с - умножение;
в) распределительная:
a(b + c) = ab+ bc,
a(b - c) = ab - ас,
a(b + c + d + ...) = ab + ac + ad +...
г) в отношении 1 и 0:
a + 0 = a; a - 0 = a;
a · 1 = a; a : 1 = a;
0 · a = 0; 0 : a = 0 |
Примеры
50 + 12 = 12 + 50
50 · 12 = 12 · 50
37 + (13 + 49) = (37 + 13) + 49 = 50 + 49 = 99;
50 · 3,5 · 2 = (50 · 2) · 3,5; 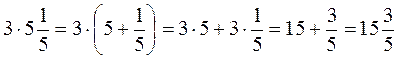 2,5 · 0,75 - 0,75 · 1,5 = =0,75 · (2,5 - 1,5) = 0,75 · 1 = 0,75 2,5 · 0,75 - 0,75 · 1,5 = =0,75 · (2,5 - 1,5) = 0,75 · 1 = 0,75 |
|
|
|
|
|
|
|
III. Повторение, систематизация знаний
Выполнение устных упражнений
2. Какие свойства действий позволяют без выполнения вычислений утверждать, что равенства являются правильными?
617 + 243 = 243 + 617; 27 · (111 + 222) = (111 + 222) · 27;
27 · (111 · 222) = (27 · 111) · 222; 27 · (111 + 222) = 27 · 111 + 27 · 222.
3. Найдите значения выражений и назовите, какое свойство было использовано:
25 · 3,18 · 4; 5,16 · 1,6 - 1,6 · 4,16; 6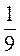 · 2.
· 2.
4. Прочитайте выражения, используя слова «сумма», «разность», «произведение», «доля»:
2,5 + 3,7; 2,5 - 3,7; 2,5 · 3,7; 2,5 : 3,7; (2,5 + 3,7)(2,5 - 3,7).
Выполнение письменных упражнений
1. Используя переставляющейся и соединительную свойства действий сложения и умножения, вычислите значения выражений наиболее рациональным способом:
1) 25 + 37 + 15 + 53; 2) 12 · 7 · 5 · 10; 3) 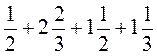 ;
;
4) 1,25 · 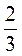 · 4 · 3; 5) 5,3 + 4,25 - 2,3 + 0,75; 6)
· 4 · 3; 5) 5,3 + 4,25 - 2,3 + 0,75; 6) 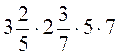 .
.
2. Используя распределительную свойство умножения относительно сложения (и вычитания), вычислите значения выражений наиболее рациональным способом:
1) 1,64 · 5,2 + 3,36 · 5,2; 2) 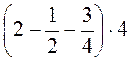 ; 3)
; 3) 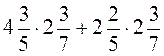 ;
;
4) 5,32 · 4,2 - 3,32 · 4,2; 5) 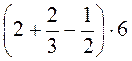 ; 6)
; 6) 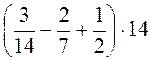 .
.
3*. Найдите значения выражений:
1) 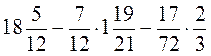 ; 2)
; 2) 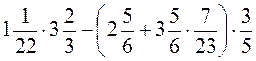 ;
;
3) 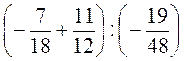 ; 4)
; 4) 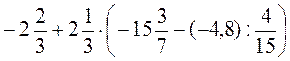 .
.
4. Запишите числовые выражения и найдите значение каждого из них:
1) произведение суммы чисел -28 и 17 число 1,2;
2) доля разности чисел 12 и 4,5 и числа -1,5;
3) сумма произведения чисел 11 и-12 и доли чисел 0,72 и-0,6;
4) квадрат суммы чисел -5,4 и 3,8.
5*. Логическое упражнение.
Установите, какой рисунок пропущено:
IV. Рефлексия
Возможен вариант проведения этого этапа урока - блиц-тест.
Выберите правильный (рациональный) вариант вычислений в выражении:
1) 25 + 7 + 5:
а)(25 + 7) + 5;
б) (25 + 5) + 7;
в) 25 + (7 + 5).
2) 25 · 7 · 4:
а) (25 · 7) · 4;
б) (25 · 4) · 7;
в) 25 · (7 · 4).
3) 3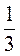 · 3:
· 3:
а) 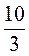 · 3;
· 3;
б) 3 · 3 + 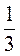 · 3;
· 3;
в) 3 · 3 + 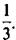
V. Домашнее задание
№ 1. Используя свойства действий, вычислите наиболее удобным способом:
1) 16 + 33 + 14 + 37;
2) 25 · 14 · 4 · 5;
3) 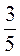 + 3
+ 3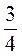 + 1
+ 1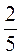 + 1
+ 1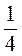 ;
;
4) 3,2 · 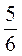 · 5 · 6;
· 5 · 6;
5) 4,7 - 2,13 + 5,3 - 2,87;
6) 2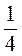 · 1
· 1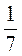 · 4 · 7;
· 4 · 7;
7) 3,81 · 4,3 + 6,19 · 4,3;
8) 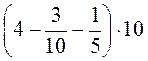 ;
;
9) 6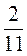 · 5
· 5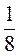 + 1
+ 1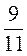 · 5
· 5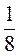 ;
;
10) 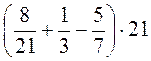 .
.
№ 2. Выполните действия: 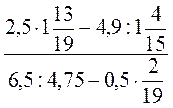 .
.
№ 3. Опережающее домашнее задание.
По учебнику или по справочникам (см. в 6 классе) повторить виды и алгоритмы преобразования буквенных выражений, что изучили в 6 классе.
_________________________________________________________
(Примечание. Задача 3* и 5* являются дополнительными, разрешаются, если позволит время, ибо основная цель урока - повторение свойств арифметических действий с рациональными числами.)
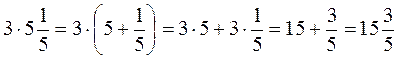 2,5
2,5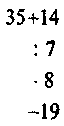
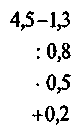
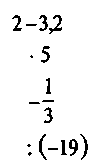
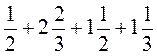 ;
;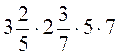 .
.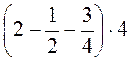 ;
;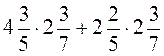 ;
;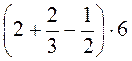 ;
; 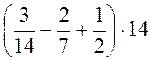 .
.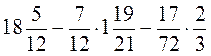 ; 2)
; 2) 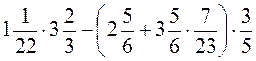 ;
;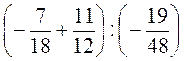 ; 4)
; 4) 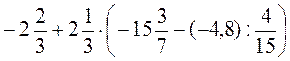 .
.