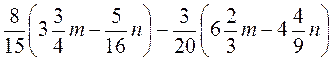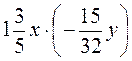|
По окончании проверяем и корегуємо выполненные задания. Вариант 2. Работа в группах. За основу берем те же самые 5 алгоритмов (см. 1-й вариант), но каждая группа получает один из алгоритмов, например, в виде набора карточек, на которых записаны отдельные части алгоритмов. Задача каждой группы состоит в том, чтобы: 1) из отдельных слов составить предложение, что выражало бы определенный алгоритм; 2) подобрать пример, иллюстрирующий применение алгоритма; 3) подготовить и осуществить презентацию своей работы. В любом случае цель этой части урока: повторить алгоритмы основных видов преобразований выражений, которые были изучены учащимися в 5-6 классах, и самое главное - воссоздать способы действий, которые предусматриваются в этих алгоритмах.
IV. Обобщение и систематизация умений и навыков Выполнение устных упражнений 1. Правильно ли раскрыты скобки? 1) 3 + (-5 - 2) = 3 - 5 - 2; 2) 3 - (5 - 2) = 3 - 5 - 2; 3) 3 - (5 + 2) = 3 + 5 - 2; 4) 3 - (5 + 2) = 3 - 5 + 2? 2. Назовите коэффициенты выражений: 3ху; -в; -1,2 а; - 3. Назовите подобные слагаемые в выражении: х - 2у +3х - у; 7b - a - 2ab + b + 3ab. 4. Раскройте скобки:(х - у) · 5; (a + b - c) · 4; -a(b + c).
Выполнение письменных упражнений 1. Упростите выражения: 1) -1,2 · 3а; 2) -5b · 2,4 с; 3) - 2. Раскройте скобки в выражениях: 1) 2(x - 7y + 3z); 2) (c- 8d + 6k) · (-1,2); 3) -b(-x + 2y - 4,6). 3. Сведите подобные слагаемые: 1) 8a + 19a - 28a + 3a; 2) 1,4 a - a + b - 2,6 b; 3) 1,6m - 1,3 - 3,1m + 0,8; 4) - 4. Раскройте скобки и сведите подобные слагаемые: 1) 7(4 + 6) - 12а; 2) 8х - 4(16 - 2х); 3) 1,7(a - 4) + 0,6(6 - 2а); 4) -(4,3х - 2,4) - (5,8 - 2,6 х); 5) 5*. Упростите выражения: 1) х - (2x - (4x + 3)); 2) 8m - (4n - 6m + (3n + 5m)). 6*. Докажите, что значение выражения не зависит от значения переменной: 1) 3(x - 2) - 5(4 + x) + 2(x + 13); 2) 2a - (a - (1 + 4a)) + 4 - a - (4a - 7). 7*. Найдите пропущенный запись:
V. Рефлексия Этот этап урока можно провести в виде игры «Корзина знаний». Каждый из учеников самостоятельно оценивает свои достижения и кладет в Корзину знаний» соответствующего цвета или формы предмет (например, если ученик считает, что материал урока усвоен им полностью, то он кладет зеленый кружок; если считает, что большинство материала усвоена, но остались некоторые непонятные моменты, то кладет желтый кружочек; если же считает, что почти все на уроке было непонятно - кладет красный кружочек). После этого учитель вместе с учениками анализирует ситуацию, которая сложилась, дает вербальную оценку результатов, выясняет, какие вопросы были самыми сложными и над чем надо более тщательно поработать дома.
VI. Домашнее задание № 1. Упростите выражения. Пронумеруйте, какие именно преобразования выражений были использованы в каждом отдельном случае. 1) -0,8 х · (-0,7); 2) 3) -7 · (5 - а - 4b); 4) -0,6 х(-5 + 3m - 1,4n); 5) -4х + 11x + 35x - 38x; 6) 1,1p + 0,9d - 1,2 - 1,3p - 3,8d; 7) 14,5(8х - 6y) - (5y - 3х) · 2,4; 8) 0,6(4х - 12) - 0,4(5х - 7). № 2. Опережающее домашнее задание. Среди математических записей один лишний. Объясните, какой и почему? 1) 3х + 2 = 5; 2) 3 + 2 = 5х; 3) 3 + 2 = 5; 4) 3х + 2х = 5. К каждой из равенств, что вы оставили, придумайте задачу. (Во время выполнения этой работы можно использовать п. 1 учебника.)
|
|