Урок № 2
Тема. Дроби. Дробные выражения. Рациональные выражения. Допустимые значения переменных
Цель: добиться усвоения учащимися терминологии, изученной на предыдущем уроке, и усвоение содержания алгоритма нахождения значений переменной, при которых данный рациональный дробь равна нулю; сформировать умение применять изученный алгоритм для решения упражнений, предполагающих нахождение значений переменных, при которых значение поданного рационального дроби равен нулю; усовершенствовать умения, формирование которых было начато на предыдущем уроке.
Тип урока: применение знаний и умений.
Наглядность и оборудование: опорный конспект «Дробные выражения. Рациональные выражения».
Ход урока
I. Организационный этап
Проверка готовности учащихся к уроку, настрой на работу.
II. Проверка домашнего задания
1. Выполнение упражнений домашней работы тщательно проверяется у учащихся, требующих дополнительного педагогического внимания (собрать тетради на проверку).
2. Математический диктант
Вариант 1
1. Запишите выражения: 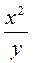 ; (х - у); (2х + у) : (2х + у);
; (х - у); (2х + у) : (2х + у); 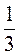 ху(х + у). Подчеркните целые выражения.
ху(х + у). Подчеркните целые выражения.
2. Можно представить выражение 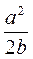 в виде многочлена?
в виде многочлена?
3. Какие допустимые значения переменной для выражения 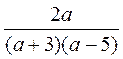 ?
?
4. Какие допустимые значения переменной для выражения (а + 3)(а - 5)?
5*. Запишите рациональный дробь, ОДЗ которого являются все числа, кроме 0 и-5.
Вариант 2
1. Запишите выражения: 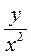 ; (x + y) : (x + y); (x - 2y)(x + 2в);
; (x + y) : (x + y); (x - 2y)(x + 2в); 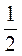 х(х - у). Подчеркните целые выражения.
х(х - у). Подчеркните целые выражения.
2. Можно ли подать выражение 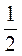 ab(x + у) в виде многочлена?
ab(x + у) в виде многочлена?
3. Какие допустимые значения переменной для выражения (х - 5)(х + 7)?
4. Какие допустимые значения переменной для выражения 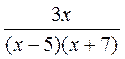 ?
?
5*. Запишите рациональный дробь, ОДЗ которого являются все числа, кроме 2 и 2.
III. Формулировка мсти и задач урока
Созданию соответствующей мотивации на уроке может способствовать выполнению учащимися задачи:
1. Найдите значения выражений 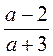 ,
, 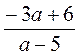 ,
, 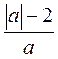 при а = 2. Сравните полученные результаты. Что вы заметили?
при а = 2. Сравните полученные результаты. Что вы заметили?
2. Существуют ли другие значения переменной а, при которых эти выражения равны нулю?
3. Или будет равна нулю при а = -2 значение выражения 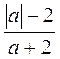 ? Почему?
? Почему?
После обсуждения результатов, полученных в ходе выполнения предложенных выше задач совместными усилиями приходим к выводу: одним из важных вопросов, связанных с понятием дробного выражения, является вопрос о условия равенства дроби нулю. Изучение этого вопроса и является основной дидактической целью урока. Задание на урок логически вытекающие из этой цели: сформулировать общее правило, а также научиться применять это правило при решении задач.
IV. Актуализация опорных знаний и умений
@ С целью успешного восприятия учащимися содержания учебного материала урока следует восстановить в памяти учащихся содержание таких понятий и алгоритмов: выполнение арифметических действий с обыкновенными дробями, преобразование целых выражений (одночлен, многочленов) в многочлен и разложения целых выражений на множители, способы решения целых уравнений, сводящихся к линейным.
Выполнение устных упражнений
1. Назовите числитель и знаменатель рациональной дроби:
а) 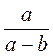 ; б)
; б) 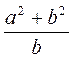 ; в)
; в) 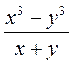 ; г)
; г) 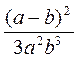 .
.
2. Решите уравнение: а) -2х = 4; б) х + 5 = 0; в) у2 = 0; г) 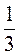 у = 3; д) 0,5 х = 5; е) х2 = -1.
у = 3; д) 0,5 х = 5; е) х2 = -1.
3. Представьте выражение в виде произведения:
а) 10х + 15у; б) а2 - 25; в) 42у2 - 21у; г) 48с - 8с2; д) 6т - 24; е) 16x - xy; ж) 27 + х3; с) а8 - а7.
4. Вычислите:
а) 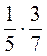 ; б)
; б) 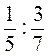 ; в)
; в) 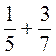 ; г)
; г) 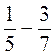 ; д) 2,3 · 3; в) 8,6 : 2; ж) 15 : 2; с) 2,1 : 2; ы) 6 : 0,3; к) 19 : 3; л)
; д) 2,3 · 3; в) 8,6 : 2; ж) 15 : 2; с) 2,1 : 2; ы) 6 : 0,3; к) 19 : 3; л) 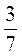 : 0,3.
: 0,3.
V. Применение знаний
План изучения нового материала
1. Условие равенства дроби нулю.
2. Алгоритм применения условия равенства дроби нулю.
3. Примеры решения задач на применение изученного алгоритма.
@ Условие равенства дроби нулю является одним из вопросов, которые предусмотрены программой по математике и имеют широкое практическое применение, поэтому уже во время первого знакомства с понятием рационального дроби следует уделить ему должное внимание.
Исходя из результатов обсуждения вопросов, предложенных на этапе мотивации учебной деятельности учащихся, сначала учитель формулирует условие равенства дроби нулю (см. опорный конспект №1) в виде системы, состоящей из двух условий: знаменатель дроби не равен нулю, числитель равен нулю.
После чего составляется примерная схема действий для решения задачи на нахождение значений переменных, при которых рациональный дробь равна нулю:
1) найти ОДЗ рационального дроби;
2) найти значения переменной, при которых числитель дроби равен нулю (приравнять числитель дроби к нулю и решить добытое уравнения);
3) выяснить, какие корни уравнения (см. предыдущий пункт) не входят в ОДЗ;
4) записать ответ - корни уравнения (см. 2 пункт), которые входят (не противоречат) ОДЗ.
После формирования алгоритма необходимо проиллюстрировать применение алгоритма на различных примерах: без наличия посторонних корней и при наличии посторонних корней.
VI. Усвоение умений
Выполнение устных упражнений
1. Из записей является условием, если дробь 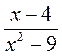 равна нулю?
равна нулю?
а) х - 4 ≠ 0; б) х2 - 9 ≠ 0; в) 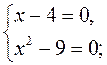 г)
г) 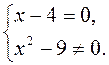
2. Составьте дробь, для которого условие равенства нулю записывается так:
а) 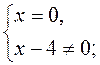 б)
б) 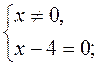 в)
в) 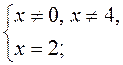 г) х = 3.
г) х = 3.
Выполнение письменных упражнений
@ 3 целью реализации дидактической цели на этом уроке следует решить задачи следующего содержания:
1. Нахождение значений переменных, при которых значение рационального дроби равен некоторому числу или нулю.
1) При каком значении переменной значение дроби 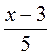 равно: а) 1; б) 0; в) -1; г) 3?
равно: а) 1; б) 0; в) -1; г) 3?
2) При каких значениях переменной значение приведенных дробей равны нулю?
а) 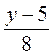 ; б)
; б) 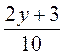 ; в)
; в)  ; г)
; г) 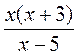 ; д)
; д) 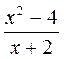 .
.
2. Нахождение ОДЗ (дробного) рационального выражения.
1) Найдите допустимые значения переменной в выражении:
а) 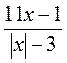 ; б)
; б) 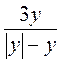 ; в)
; в) 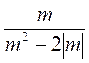 ; г)
; г) 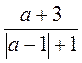 .
.
2) Укажите допустимые значения переменной в выражении:
а) х2 - 8х + 9; б) 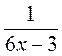 ; в)
; в) 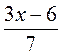 ; г)
; г) 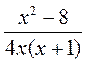 ; д)
; д) 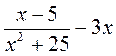 ; е)
; е) 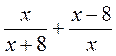 .
.
3) Найдите область определения функции:
а) 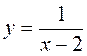 ; б)
; б) 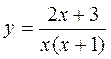 ; в)
; в) 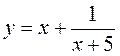 .
.
3. Нахождение значения дробного выражения при данных значениях переменной (переменных).
Найдите значение выражения 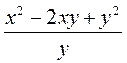 : а) х = 44, у = 4; б) х = 46, в = 46; в) х = 1,25, в = 0,25.
: а) х = 44, у = 4; б) х = 46, в = 46; в) х = 1,25, в = 0,25.
4. Составление выражений по текстовой условием и вычисления значение составленного выражения при заданных значениях переменных.
1) Составьте выражение для решения задачи.
Катер проплыл 25 км по течению реки и 20 км против течения. Найдите время движения катера, если его скорость в стоячей воде v км/ч, а скорость течения реки км/ч.
2) Составьте выражение для решения задачи.
Поезд за определенное время должен был преодолеть путь 250 км, двигаясь со скоростью а км/ч. Но через 2 часа он был задержан. Поэтому, чтобы прибыть к месту назначения вовремя, он увеличил скорость на 25 км/ч. Найдите длительность задержки.
5. Выполнение упражнений на преобразование целых выражений с применением алгоритмов, изученных в 7 классе.
Разложите на множители:
а) a2b + ab2;
б) х3у - ху3;
в) 7х2 - 14ху + 21ах;
г) 9ху - 3bв + 15ау;
д) х4 - х3 + х2 - х;
есть) с4 - 2с3 - с2 + 2с;
ж) (а - 2)2 - 25а2;
с) (b + 3)2 - 36b2;
ы) 125x3 + 8;
к) 216х3 - 27;
л) (а + 1)3 + а3;
г) (b + 2)3 - 863.
6. Для учащихся, имеющих достаточный и высокий уровень знаний - выполнение логических упражнений и задания повышенного уровня сложности.
1) Составьте дробь, содержащее переменную х в знаменателе и имеет смысл при всех значениях х.
2) Докажите тождество:
а) а4 + а2 + 1 = (а2 + а + 1)(а2 - а + 1);
б) b8 + b4 + 1 = (b4 + b2 + 1)(b4 - b2 + 1);
в) с4 + 4 = (с2 - 2с + 2)(с2 + 2с + 2).
3) Найдите пропущенный выражение:
28 |
a2 - (b - с)2 |
2 · 2 · 7 |
7 |
VII. Итоги урока
Среди предложенных чисел выберите те, что удовлетворяют условие для дроби:
а) дробь 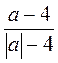 существует;
существует;
б) дробь 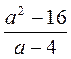 равна нулю.
равна нулю.
Числа: 4; -4; 16; -16.
VIII. Домашнее задание
1. Изучить содержание условия, когда дробь равна нулю, повторить определение рационального дроби, ОДЗ выражения.
2. Выполнить упражнения на закрепление алгоритма нахождения значений переменных, при которых дробь равна нулю и повторение алгоритма нахождения ОДЗ выражения.
3. На повторение: повторить сокращение дробей и разложение многочленов на множители, деление степеней с натуральным показателем.
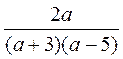 ?
?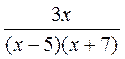 ?
?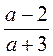 ,
, 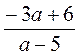 ,
, 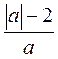 при а = 2. Сравните полученные результаты. Что вы заметили?
при а = 2. Сравните полученные результаты. Что вы заметили?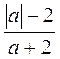 ? Почему?
? Почему?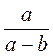 ; б)
; б) 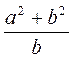 ; в)
; в) 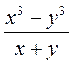 ; г)
; г) 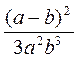 .
.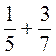 ; г)
; г) 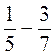 ; д) 2,3 · 3; в) 8,6 : 2; ж) 15 : 2; с) 2,1 : 2; ы) 6 : 0,3; к) 19 : 3; л)
; д) 2,3 · 3; в) 8,6 : 2; ж) 15 : 2; с) 2,1 : 2; ы) 6 : 0,3; к) 19 : 3; л) 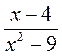 равна нулю?
равна нулю?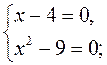 г)
г) 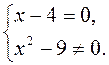
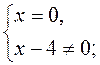 б)
б) 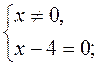 в)
в) 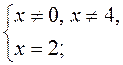 г) х = 3.
г) х = 3.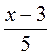 равно: а) 1; б) 0; в) -1; г) 3?
равно: а) 1; б) 0; в) -1; г) 3?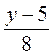 ; б)
; б) 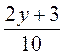 ; в)
; в)  ; г)
; г) 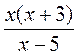 ; д)
; д) 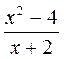 .
.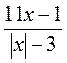 ; б)
; б) 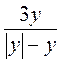 ; в)
; в) 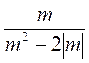 ; г)
; г) 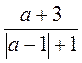 .
.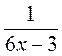 ; в)
; в) 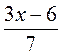 ; г)
; г) 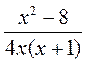 ; д)
; д) 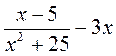 ; е)
; е) 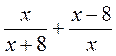 .
.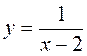 ; б)
; б) 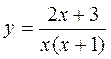 ; в)
; в) 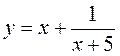 .
.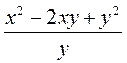 : а) х = 44, у = 4; б) х = 46, в = 46; в) х = 1,25, в = 0,25.
: а) х = 44, у = 4; б) х = 46, в = 46; в) х = 1,25, в = 0,25.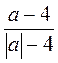 существует;
существует;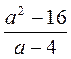 равна нулю.
равна нулю.