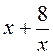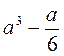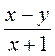Урок № 1
Тема. Дроби. Дробные выражения. Рациональные выражения. Допустимые значения переменных
Цель: добиться усвоения учащимися содержания понятий: целое выражение, дробное выражение, рациональное выражение, рациональное дробь, допустимые значения переменной в выражении; сформировать у учащихся умения выделять названные виды выражений среди предложенных выражений с переменными, а также выполнять действия, которые имеют целью нахождение ОДЗ дробного выражения.
Тип урока: усвоение знаний, умений и навыков.
Наглядность и оборудование: опорный конспект «Дробные выражения. Рациональные выражения».
Ход урока
I. Организационный этап
Вступительное слово учителя
· Особенности изучения алгебры в 8 классе;
· организация учебного процесса;
· строение учебника.
II. Проверка домашнего задания
Учитель проверяет летнее домашнее задание (если такое было задано).
III. Формулировка цели и задач урока
С целью осознания учащимися необходимости изучения вопроса о видах рациональных выражений предлагаем учащимся задание:
Какой из выражений: х2, х + 2ху, 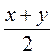 ,
, 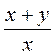 лишний? Почему?
лишний? Почему?
После обсуждения с учащимися результатов выполнения предложенного задания формируется мнение: в 7 классе был изучен вопрос о виды, свойства и способы преобразования выражений, не содержит деления на переменную (целые выражения); в 8 классе пришло время изучить виды, свойства и способы преобразований выражений, содержащих деление на переменную(дробные выражения), а также обобщить знания учащихся о видах выражений и логическую связь между ними. Этот вывод и является основной дидактической целью изучения раздела.
IV. Актуализация опорных знаний и умений
@ целях успешного восприятия учащимися учебного материала урока перед изучением новой темы следует активизировать знания учащихся о алгоритмы выполнения действий с рациональными числами, способы преобразования целых рациональных выражений и способы решения линейных уравнений и уравнений, сводящихся к линейным (изученные в 7 классе).
Выполнение устных упражнений
1. Найдите значения выражений:
1 - 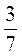 ;
; 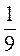 - 2;
- 2; 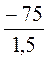 ; -27 : 81; -3,7 - 0,4;
; -27 : 81; -3,7 - 0,4; 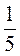 - 0,2;
- 0,2; 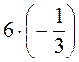 ;
; 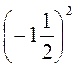 .
.
2. Вычислите:
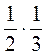 ;
; 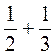 ;
; 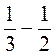 ;
; 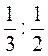 ;
; 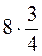 ;
; 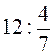 ; 19 · 0,1; 7 : 0,1;
; 19 · 0,1; 7 : 0,1; 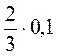 ;
; 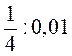 .
.
3. При каком значении переменной значение выражения равно нулю:
х - 1; у + 3, а2 х2 + 4; а(а - 1); х(х + 3); 2x - 1; 5в(в + 1); |х|; |х - 3|; |х| - 1?
4. Упростите выражения: х5 · х; 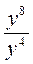 ; 5 - (х + 3); 2,5 + (у - 0,5).
; 5 - (х + 3); 2,5 + (у - 0,5).
5. Представьте выражения в виде произведения:
а2 - b2; ху - х2; а2b - аb; х3 - у3; с2 - 2cd + d2; а3 + b3.
6. Преобразуйте выражения в многочлен стандартного вида:
а(а - 3); -с(х - у + а); (х + 1)(х - 3); (а - 4)(4 + а); (х+2)2; (а - b)(а2 + аb + b2).
V. Усвоение знаний
План изучения нового материала
1. Целые выражения.
2. Дробные выражения.
3. Рациональные выражения.
4. Рациональный дробь.
5. Допустимые значения переменных в выражении (ОДЗ).
Конспект 1 |
Дробные выражения. Рациональные выражения |
1. Целые выражения состоят из чисел, букв и степеней и действий сложения, вычитания, умножения, возведения в степень и деления, кроме деления на переменную. |
Пример. a + b; 2а3; 3х(х - в)3; b; 5 - целые выражения. |
!Любое целое выражение можно представить в виде многочлена. |
2. Дробные выражения обязательно содержащие действие деления на выражение с переменной (переменными), а также могут содержать все действия, которые есть в целом выражении. |
Пример. 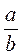 ; ; 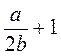 ; ; 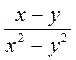 ; 5х : у - дробные выражения. ; 5х : у - дробные выражения. |
3. Целые выражения вместе с дробными выражениями называют рациональными выражениями. |
4. Запись 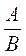 , где А и В - некоторые буквенные или числовые выражения, называют дробью. , где А и В - некоторые буквенные или числовые выражения, называют дробью. |
Дробь 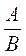 , где А и В - многочлены называют рациональной дробью. , где А и В - многочлены называют рациональной дробью. |
Пример. 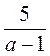 ; ; 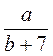 ; ; 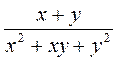 - рациональные дроби. - рациональные дроби. |
5. Область допустимых значений переменных в выражении (ОДЗ) - все такие значения переменных, при которых выражение имеет смысл. |
!Для рационального дроби 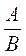 допустимые значения переменной определяются из условия В ≠ 0 (знаменатель не должен равняться 0). допустимые значения переменной определяются из условия В ≠ 0 (знаменатель не должен равняться 0). |
Пример. Для выражения 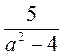 допустимы все значения а, кроме тех, при которых а2 - 4 = 0, то есть (а - 2)(а + 2) = 0, т.е. а = 2 или а = -2. допустимы все значения а, кроме тех, при которых а2 - 4 = 0, то есть (а - 2)(а + 2) = 0, т.е. а = 2 или а = -2. |
Итак, ОДЗ переменной а в выражении 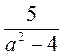 можно записать так: можно записать так: |
ОДЗ: а ≠ ±2 (или а ≠ 2 и а ≠ -2, или все значения а, кроме а = 2 и а = -2). |
6. Рациональный дробь 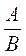 равна 0, тогда и только тогда, когда А = 0 и В ≠ 0 (или равна 0, тогда и только тогда, когда А = 0 и В ≠ 0 (или 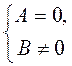 ) ) |
Чтобы найти значение переменной, при котором рациональный дробь 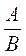 равна 0, надо: равна 0, надо: |
а) найти ОДЗ дроби (из условия В ≠ 0); |
б) приравнять числитель к нулю (А = 0) и найти соответствующие значения переменных; |
в) из значений, полученных в п. б) исключить те, что не входящие в ОДЗ (см. п. а.). |
Пример. При каком значении переменной дробь 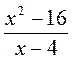 равна нулю? равна нулю? |
Решение |
1) ОДЗ: х - 4 ≠ 0; х ≠ 4; |
2) х2 - 16 = 0; (х - 4)(х + 4) = 0; х = 4 или х = - 4. |
3) х = 4 не входит в ОДЗ, поэтому при х = - 4 дробь 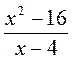 равна нулю. равна нулю. |
@ Изучения материала урока начинается с повторения видов целых выражений, которые изучали ученики в 7 классе (одночлен, многочлены), и обобщение представлений учащихся об их структуру и свойства (все целые выражения содержат 5 арифметических действий, кроме деления на выражение с переменными, и могут быть представлены в виде многочлена).
Как противоположность целым выражениям рассматриваются выражения, что, кроме других арифметических действий, содержит деления на переменную - таким образом формируется представление учащихся о содержании понятия дробного выражения, после чего рассматривается понятие рационального выражения как общего вида выражений, делится на целые и дробные выражения.
Далее формируется представление учащихся о содержании понятия рационального дроби как особого случая дробного выражения и о содержании понятия допустимого значения переменной в выражении и области допустимых значений переменной (ОДЗ) в выражении (при этом можно опираться на приобретенные учащимися в 7 классе знания о содержании понятия области определения функции).
VI. Усвоение знаний и умений
Выполнение устных упражнений
1. Какие из выражений являются целыми; дробными? Какие из выражений являются дробями; рациональными дробями?
а) 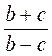 ; б)
; б) 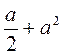 ; в)
; в) 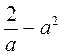 ; г)
; г) 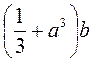 ; д)
; д) 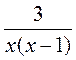 ; е)
; е) 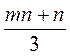 .
.
2. Найдите значение выражения 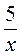 при х = 5, х = -5, х = -0,1.
при х = 5, х = -5, х = -0,1.
3. При каких значениях переменной выражение не имеет смысла? Назовите допустимые значения переменной в выражении:
а) 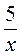 ; б)
; б) 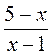 ; в)
; в) 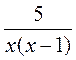 ; г)
; г) 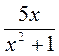 .
.
4. Какие из приведенных равенств является тождественностями?
а) 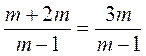 ; б)
; б) 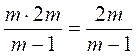 ; в)
; в) 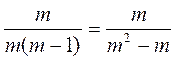 .
.
Выполнение письменных упражнений
@ Для реализации дидактической цели на этом уроке следует решить задачи следующего содержания:
1. Среди представленных выражений с переменными выбрать: целые, дробные выражения, рациональные дроби.
1) Какие из выражений являются целыми; дробными? Какие из выражений являются дробями; рациональными дробями?
а) 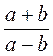 ; б)
; б) 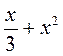 ; в)
; в) 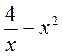 ; г)
; г) 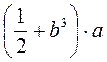 ; д)
; д) 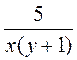 ; е)
; е) 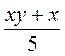 .
.
2) Какие из выражений 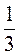 а2b; (х - у)2 - 4ху;
а2b; (х - у)2 - 4ху; 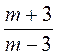 ;
; 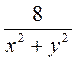 ;
; 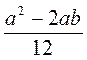 ; (с + 3)2 +
; (с + 3)2 + 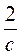 являются целыми, дробными?
являются целыми, дробными?
3) Из рациональных выражений 7х2 - 2ху; 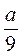 ;
; 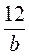 ; а(а - b) -
; а(а - b) - 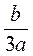 ;
; 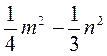 ;
; 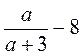 выпишите те, которые являются:
выпишите те, которые являются:
а) целыми выражениями; б) дробными выражениями.
4) Составьте дробь:
а) числитель которого является произведением переменных х и у, а знаменатель - сумме;
б) числитель которого является разницей переменных а и b, а знаменатель - произведением.
2. Нахождение значения дробного выражения при данных значениях переменных.
1) Найдите значение выражения:
а) 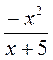 при x = 0; х = 5; х = -3;
при x = 0; х = 5; х = -3;
б) 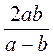 при а = 4, b = 2; а = -4, b = 6;
при а = 4, b = 2; а = -4, b = 6;
в) 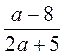 при а = -2;
при а = -2;
г) 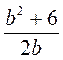 при b = 3;
при b = 3;
д) 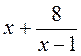 при x =
при x = 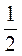 ;
;
есть) 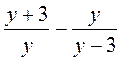 при в = 1,5.
при в = 1,5.
2) Чему равно значение дроби 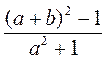 при:
при:
а) a = -3, b = -1; б) a = 1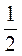 , b = 0,5?
, b = 0,5?
3. Нахождение допустимых значений переменных в выражении.
1) Укажите допустимые значения переменной в выражении:
а) 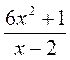 ; б)
; б) 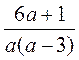 ; в)
; в) 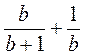 ; г)
; г) 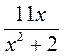 .
.
2) Найдите допустимые значения переменной в выражении:
а) 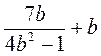 ; б)
; б) 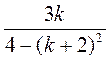 ; в)
; в) 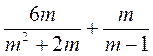 .
.
4. Составление выражений с переменными по условию задачи.
Автомобиль проехал 195 км за? ч. Запишите в виде выражения скорость автомобиля. Найдите значение этого выражения при t = 3. Выполнение упражнений на повторение: арифметические действия с обыкновенными дробями (сокращение, сравнение, сложение, вычитание, разложение целых выражений на множители с применением различных способов.
1) Преобразуйте в многочлен:
а) (х - 10)(х + 10);
б) (2а + 3)(2а - 3);
в) (y - 5b)(y + 5b);
г) (8x + y)(y - 8x);
д) (х + 7)2;
есть) (b + 5)2;
ж) (а - 2х)2;
с) (ab - 1)2.
2) Разложите многочлен на множители:
а) 15ах + 20ау; б) 36bв - 9су; в) х2 - ху; г) ху - у2; д) а2 +5ab; е) 15с - 10с2.
3) Разложите на множители:
а) х2 - 25; б) 16 - с2; в) а2 - 6a + 9; г) х2 + 8х + 16; д) а3 - 8; е) b3 + 27.
5. Для учащихся, имеющих достаточный и высокий уровень знаний - выполнение заданий повышенного уровня сложности и логические упражнения. Вставьте пропущенный выражение:
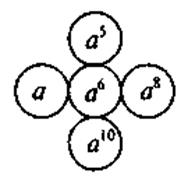
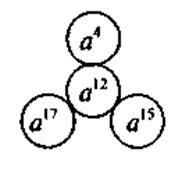
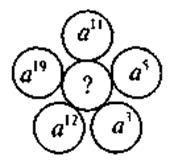
VII. Итоги урока
Контрольные вопросы
1) Какие выражения называют целыми? Приведите примеры.
2) Какие выражения называют дробными? Приведите примеры.
3) Какие выражения называют рациональными? Какие из приведенных рациональных выражений целые, а дробные: 3а, 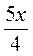 ,15р2q,
,15р2q, 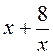 ,
, 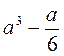 ,
, 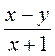 ?
?
VIII. Домашнее задание
1. Изучить определения понятий, рассмотренных на уроке.
2. Решить упражнения на: классификацию рациональных выражений, нахождение ОДЗ выражений, вычисление значений выражений с переменными, числовых выражений, содержащих обыкновенные дроби, решение целых уравнений.
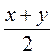 ,
, 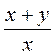 лишний? Почему?
лишний? Почему?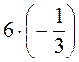 ;
; 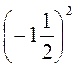 .
.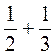 ;
; 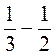 ;
; 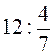 ; 19 · 0,1; 7 : 0,1;
; 19 · 0,1; 7 : 0,1; 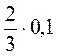 ;
; 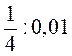 .
.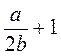 ;
; 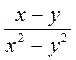 ; 5х : у - дробные выражения.
; 5х : у - дробные выражения.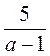 ;
; 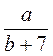 ;
; 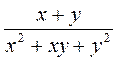 - рациональные дроби.
- рациональные дроби.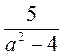 допустимы все значения а, кроме тех, при которых а2 - 4 = 0, то есть (а - 2)(а + 2) = 0, т.е. а = 2 или а = -2.
допустимы все значения а, кроме тех, при которых а2 - 4 = 0, то есть (а - 2)(а + 2) = 0, т.е. а = 2 или а = -2.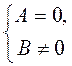 )
)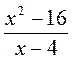 равна нулю?
равна нулю?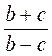 ; б)
; б) 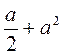 ; в)
; в) 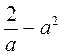 ; г)
; г) 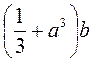 ; д)
; д) 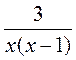 ; е)
; е) 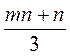 .
.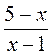 ; в)
; в) 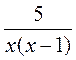 ; г)
; г) 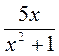 .
.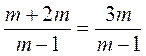 ; б)
; б) 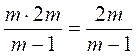 ; в)
; в) 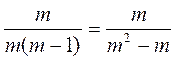 .
.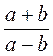 ; б)
; б) 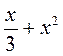 ; в)
; в) 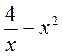 ; г)
; г) 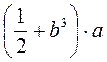 ; д)
; д) 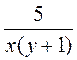 ; е)
; е) 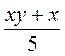 .
.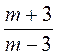
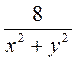
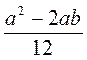 ; (с + 3)2 +
; (с + 3)2 + 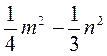 ;
; 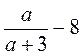 выпишите те, которые являются:
выпишите те, которые являются: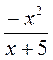 при
при 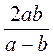 при а = 4,
при а = 4, 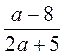 при а = -2;
при а = -2; 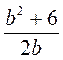 при
при 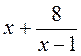 при
при 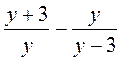 при в = 1,5.
при в = 1,5.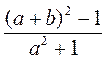 при:
при: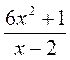
 .
.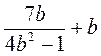 ; б)
; б) 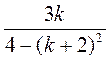 ; в)
; в) 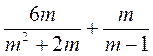 .
.