|
2. Какой из приведенных выражений имеет смысл при любом значении переменной х?
3. При каком значении х дробь
4. При каком значении х дробь
Вариант 2 1. Какое из приведенных выражений является целым выражением?
2. Какой из приведенных выражений имеет смысл при любом значении переменных?
3. При каком значении х дробь
4. При каком значении х дробь
III. Формулировка цели и задач урока На этом этапе урока будет уместным слово учителя о том, что обычные и рациональные дроби имеют одинаковое основное свойство и общие правила выполнения арифметических действий. Понятно, что работу с изучения действий над рациональными дробями следует начинать с основного свойства - именно ее изучения и представляет основную дидактическую цель урока. Задачами на урок является: сформулировать алгоритмы применения основного свойства рационального дроби на основе выполнения действий с многочленами. Как вариант работы с детьми, которые имеют высокий уровень интеллектуальной деятельности, предлагаем задания. Найдите значения выражений После обсуждения результатов проделанной работы появляется гипотеза о том, что значение рациональных дробей не изменится во время выполнения деления или умножения числителя и знаменателя дроби на одно и то же выражение, что не равна нулю. Подтверждение этой гипотезы и является основной целью урока.
IV. Актуализация опорных знаний и умений @ Для подготовки учащихся к восприятию нового материала целесообразно решить устные упражнения на повторение алгоритмов выполнения арифметических действий с рациональными числами, алгоритмов преобразований целых выражений, изученных в 7 классе (особенно различных способов разложения многочленов на множители), а также материала, изученного на предыдущих уроках в 8 классе (нахождение ОДЗ рационального выражения). Выполнение устных упражнений 1. Сократите дроби: 2. Сведите дроби к знаменателю 36; 3. Вычислите: 4. Представьте выражения в виде произведения: 25 - у2; a2 + ab; 8 + х3; 1 + а2 - 2а; 3х6 - 12x2; b10 - b2. 5. Представьте число 3 в виде дроби со знаменателем: 2; 5; 1; 4; 10. 6. Среди выражений: х + у; х + у; х - у; в - х; х - у; (х - у)2; (у - х)2; (- х - у)2; (х + у)2; (-х - у)3; (х - у)2; -(х + у)3; - (х - у)3 найдите: а) тождественно равны; б) противоположные. Докажите.
V. Усвоение знаний План изучения нового материала 1. Представление о основное свойство обыкновенной дроби; ее адаптация на рациональный дробь (с доводкой). 2. Основное свойство дроби и сокращение дробей. Алгоритм рационального сокращения дроби. 3. Основное свойство дроби и правило знаков.
@ Изложения учебного материала урока следует начать с формулировки и доказательство основного свойства рационального дроби, которая подается как в математическом ( Доведение свойства опирается на представление о дробь как запись доли от деления двух выражений и на зависимость между компонентами действия деления. После формирования у учеников представления о «две стороны» основного свойства рационального дроби подается название одного из преобразований, входящих в основного свойства дроби, сокращения дробей; при этом подчеркивается, что под сокращением дробей понимают деления числителя и знаменателя рациональной дроби на общий множитель числителя и знаменателя, поэтому сокращение рациональных дробей предусматривает выполнение определенных действий в определенной последовательности для выделения этого общего множителя. Составляется алгоритм сокращения рациональная дробей. Во время решения примеров на применение составленного алгоритма сокращения дробей можно предложить упражнения, которые подготовят учащихся к восприятию правила знаков для рациональных дробей (или до самостоятельного составления этого правила в случае высокого уровня подготовки учащихся к самостоятельной интеллектуальной деятельности). После формулировки общего правила рассматриваются примеры, при решении которых необходимо использовать правило знаков, и комментируются общие способы действий в случае применения этого правила (если на обработку правила знаков не хватит времени на уроке № 3, можно рассмотреть его на уроке № 4 вместе с вопросом о возведении дроби к новому знаменателю).
VI. Усвоение умений Выполнение устных упражнений 1. Какие из дробей 2. Назовите общий множитель числителя и знаменателя дроби и сократите дроби:
3. Верны ли равенства: а)
Выполнение письменных упражнений @ Для реализации дидактической цели на этом уроке следует решить задачи следующего содержания: 1. Сокращение рационального дроби. 1.1. На одночлен. 1) Выделите общий множитель числителя и знаменателя дроби и сократите дробь: а) 2) Сократите дробь: а) 1.2. На многочлен (который уже выделено в числителе и знаменателе поданных рациональных дробей). 1) Сократите дробь: а) 2) Сократите дробь: а)
2. Сокращение рационального дроби с предварительным разложением числителя и знаменателя на множители. 1) Разложите на множители числителя и знаменателя и сократите дробь: а) 2) Сократите дробь: а) 3) Разложите на множители числителя и знаменателя и сократите дробь: а) 4) Сократите дробь: а)
3. Выполнение упражнений на правила использования знаков перед сокращением дробей. 1) Упростите выражение: а) 2) Сократите дробь: а)
4. Нахождение значений рациональных дробей с предварительным их сокращением. 1) Найдите значение выражения: а) б) 15x2y3 : (30xy2) при х = 300, у = 0,06. 2) Найдите значение выражения 5. Выполнение упражнений на повторение: упражнения на нахождение ОДЗ дроби и условия равенства дроби нулю. 1) Найдите допустимые значения переменной в выражении: а) 2) Составьте дробь с переменной х, которое имеет смысл при всех значениях переменной, кроме: а) х = 2; б) х = 0 и х = 3; в) х = -3 и х = 3; г) х = 6. Выполнение логических упражнений и заданий повышенного уровня сложности для учащихся, имеющих достаточный и высокий уровень знаний. 1) Сократите дробь: а) 2) Найдите пропущенный выражение:
VII. Итог урока Какое равенство является записью правильно выполненного сокращение рациональных дробей? а)
VIII. Домашнее задание 1. Изучить содержание основного свойства дроби и алгоритма ГГ применения для сокращение рациональных дробей. 2. Решить упражнения на сокращение дробей (уровня, что соответствует упражнениям классной работы). 3. На повторение: нахождение значений переменных, при которых дробь равна нулю, и повторение алгоритма нахождения ОДЗ выражения.
|
|
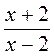
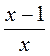
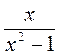
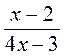 не существует?
не существует?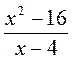 равна нулю?
равна нулю?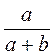
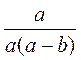
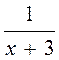
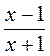
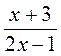 не существует?
не существует?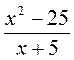 равна нулю?
равна нулю?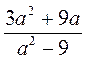 и
и 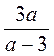 при а = 4. Сравните полученные результаты. Сравните выражения. Что вы заметили?
при а = 4. Сравните полученные результаты. Сравните выражения. Что вы заметили?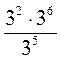 ;
; 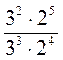 ;
; 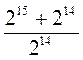 .
.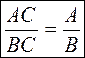 - правило сокращения дробей.
- правило сокращения дробей.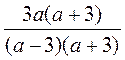 .
.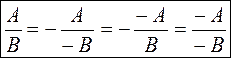 - правило знаков.
- правило знаков.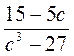 .
.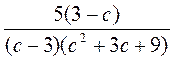 .
.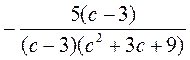 .
.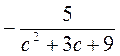 .
.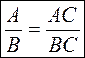 - расширение дроби (возведение дроби к новому знаменателю).
- расширение дроби (возведение дроби к новому знаменателю). 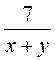 к знаменателю х2 + ху.
к знаменателю х2 + ху.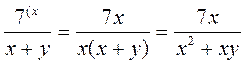 .
.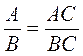 ,
,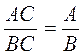 , где А, В, С - некоторые многочлены, причем В ≠ 0, С ≠ 0), так и в словесном виде.
, где А, В, С - некоторые многочлены, причем В ≠ 0, С ≠ 0), так и в словесном виде.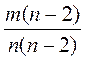 ;
; 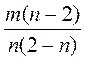 ;
; 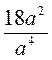 .
.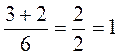 ; б)
; б) 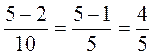 ; в)
; в) 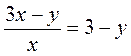 ; г)
; г) 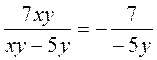 ?
?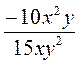 .
.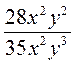 ; б)
; б) 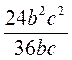 ; в)
; в) 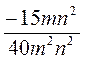 ; г)
; г) 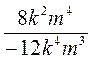 .
.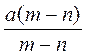 ; б)
; б) 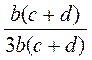 ; в)
; в) 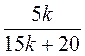 ; г)
; г) 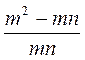 .
.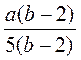 ; б)
; б) 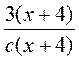 ; в)
; в) 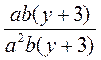 ; г)
; г) 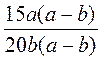 .
.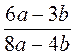 ; б)
; б) 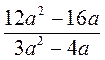 ; в)
; в) 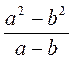 ; г)
; г) 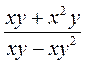 .
.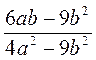 ; б)
; б) 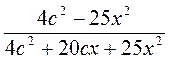 ; в)
; в) 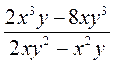 .
.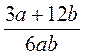 ; б)
; б) 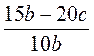 ; в)
; в) 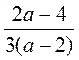 ; г)
; г) 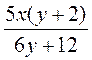 ; д)
; д) 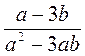 ; е)
; е) 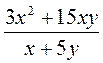 .
.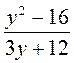 ; б)
; б) 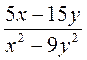 ; в)
; в) 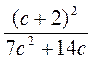 ; г)
; г) 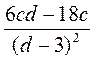 ; д)
; д) 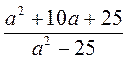 ; е)
; е) 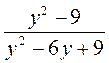 .
.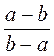 ; б)
; б) 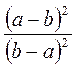 ; в)
; в) 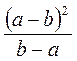 ; г)
; г) 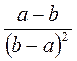 ; д)
; д) 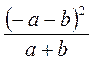 ; е)
; е) 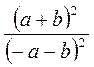 .
.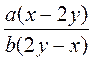 ; б)
; б) 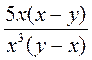 ; в)
; в) 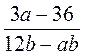 ; г)
; г) 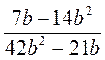 ; д)
; д) 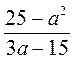 ; е)
; е) 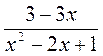 ; ж)
; ж) 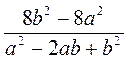 ; з)
; з) 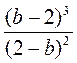 .
.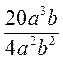 при а = 48,
при а = 48, 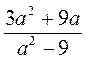 при а = 4; а =
при а = 4; а = 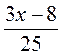 ; б)
; б) 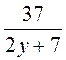 ; в)
; в) 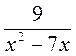 ; г)
; г) 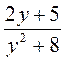 ; д)
; д) 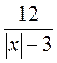 ; е)
; е) 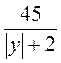
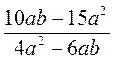 ; б)
; б) 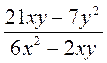 ; в)
; в) 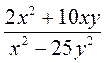 ; г)
; г) 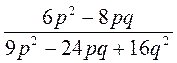 ; д)
; д) 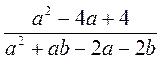 ; е)
; е) 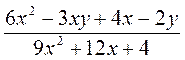 ; ж)
; ж) 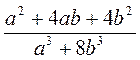 ; з)
; з) 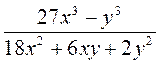 .
.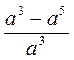
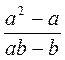
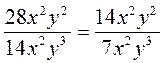 ; б)
; б) 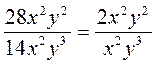 ; в)
; в) 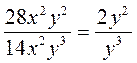 ; г)
; г) 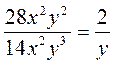 .
.