АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел II. УРАВНЕНИЯ И НЕРАВЕНСТВА

§21. АРКСИНУС, АРККОСИНУС, АРКТАНГЕНС И АРККОТАНГЕНС ЧИСЛА.

2. Арктангенс и арккотангенс.

Арктангенсом числа а, где а - любое число, называют такое число (угол) из промежутка (-π/2; π/2), тангенс которого равен а.

Обозначают арктангенс числа а так аrctg а. Из определения следует, что arctg а = φ тогда и только тогда, когда:

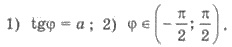
Пример 1.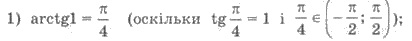

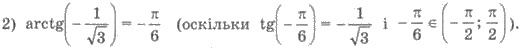
Арккотангенсом числа а, где а - любое число, называют такое число (угол) из промежутка (0;π), котангенс которого равен а.

Обозначают арккотангенс числа а так аrсctg а. Из определения следует, что arcctg a = φ тогда и только тогда, когда:

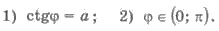
Пример 2.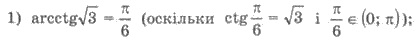

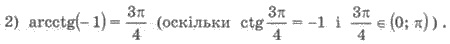
Полезной является таблица значений аrctg а и аrссtg а для некоторых значений а.