АЛГЕБРА И НАЧАЛА АНАЛИЗА
Раздел II. УРАВНЕНИЯ И НЕРАВЕНСТВА
§21. АРКСИНУС, АРККОСИНУС, АРКТАНГЕНС И АРККОТАНГЕНС ЧИСЛА.
1. Арксинус и арккосинус числа.
Арксинусом числа а, где |а| ≤ 1, называют такое число (угол) с
промежутке [-π/2; π/2], синус которого равен а.
Обозначают арксинус числа а так arcsin a. Из определения следует, что arcsin а = φ
тогда и только тогда, когда:

Пример 1.
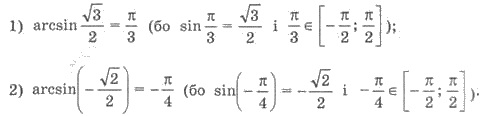
Арккосинусом числа а, где |а| ≤ 1, называют такое число (угол) с
промежутке [0;π],
косинус которого равен а.
Обозначают арккосинус числа а так arccos а. Из определения следует, что arccos а = φ
тогда и только тогда, когда:
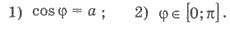
Пример 2.
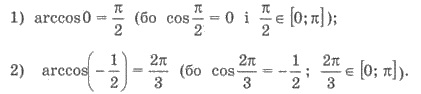
Полезной является таблица значений arcsin а и arccos а для некоторых значений а.
|
а
|
-1
|
- /2 /2
|
-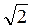 /2 /2
|
-1/2
|
0
|
1/2
|
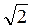 /2 /2
|
 /2 /2
|
1
|
|
аrсsиn а
|
- π/2
|
- π/3
|
- π/4
|
- π/6
|
0
|
π/6
|
π/4
|
π/3
|
π/2
|
|
аrуснs
а
|
π
|
5π/6
|
3π/4
|
2π/3
|
π/2
|
π/3
|
π/4
|
π/6
|
0
|