Прямая и обратная теоремы

Формулировка теоремы состоит из двух частей. В одной говорится о том, что дано. Эта часть называется условием. Во второй части говорится о том, что надо доказать. Эта часть называется выводом.
Примеры
1) Если углы смежные, то их сумма равна 180°.

Условие Заключение
2) В прямоугольном треугольнике центр описанной окружности - середина гипотенузы.
Условие: треугольник является прямоугольным.
Вывод: центр описанной окружности - середина гипотенузы.
3) Две прямые, параллельные третьей, параллельны друг другу.
Дано (условие): прямые a, b, c; ;.
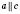
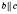
Доказать (вывод): .
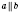
Если условия и заключение теоремы поменять местами, получим теорему, которая называется обратной к данной («прямой») теоремы. Следующие две теоремы называют взаємооберненими. Каждую из них можно назвать прямой, тогда другая будет обратной. Иногда из этих двух теорем правильной является только одна.
Пример
Прямая теорема. Если углы вертикальные, то они равны. (Правильно.)
Обратная теорема. Если углы равны, то они вертикальные. (Неверно.)
Бывают случаи, когда правильными являются обе теоремы.
Пример
Прямая теорема. Углы при основании равнобедренного треугольника равны. (Правильно.)
Обратная теорема. Если два угла треугольника равны, то он равнобедренный. (Правильно.)
В таких случаях используют словосочетание «тогда и только тогда», «необходимо и достаточно».
Примеры
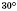
1) Катет прямоугольного треугольника тогда и только тогда равен половине гипотенузы, когда противоположный ему угол равен . (Это утверждение содержит одновременно прямую и обратную теоремы.)
2) Для того чтобы прямые были параллельны, необходимо и достаточно, чтобы внутренние разносторонние углы были ровными.
Надо понимать, что утверждение «для того чтобы прямые были параллельны, необходимо, чтобы внутренние разносторонние углы были ровными» означает свойство параллельных прямых.
Утверждение «для того чтобы прямые были параллельными, достаточно, чтобы внутренние разносторонние углы были ровными» означает признак параллельных прямых.