АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел II. УРАВНЕНИЯ И НЕРАВЕНСТВА

§7. РЕШЕНИЕ УРАВНЕНИЙ, СВОДЯЩИХСЯ К КВАДРАТНЫМ.

3. Біквадратні уравнения.

Уравнение вида ах⁴ + bх² + с = 0, где а 0, называют біквадратним уравнением. Это уравнение можно решить, вводя новую переменную, а именно, обозначив х² через t. Тогда исходное уравнение примет вида аt² + bt + c = 0.

Пример. Решите уравнение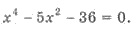

Решения. Сделаем замену х² = t, тогда имеем уравнение 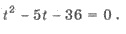Это уравнение имеет корни t₁ = 9; t₂ = -4.

Вернемся к переменной х.

1) t₁ = 9, тогда х² = 9; х₁ = 3; х₂ = -3.

2) t₂ = -4, тогда х² = -4, то уравнение не имеет решений.

Следовательно, исходное уравнение имеет корни х₁ = 3; х₂ = -3.