Применение производной
Пусть функция
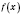
определена на промежутке
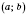
и
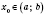
.
Функция называется
возрастающей в точке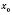
, если существует интервал
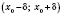
, где
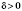
, который содержится в промежутке
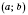
и является таким, что
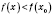
для всех
x из интервала
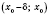
и
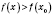
для всех
x из интервала
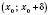
.
Функция называется
убывающей в точке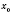
, если существует интервал
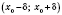
, который содержится в промежутке
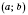
и является таким, что
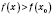
для любого
x из интервала
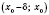
и
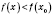
для любого
x из интервала
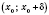
.
Определение точек экстремума описано в разделе «Алгебра. 10 класс».
Если функция
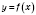
возрастающая (убывающая) в каждой точке промежутка
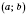
, то она возрастающая (убывающая) на этом промежутке.
Теорема 1. Если функция
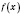
в каждой точке интервала
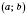
имеет производную
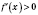
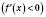
, то функция возрастает (убывает) на
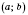
.
Обратите внимание:
1) Если функция
f является непрерывной в каком-то из концов интервала
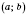
, то эту точку можно присоединить до интервала возрастания (убывания).
2) Для решения задач удобно пользоваться таким утверждением: точки, в которых производная равна 0 или не существует, делят область определения функции
f на промежутки, в каждом из которых
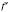
сохраняет неизменный знак.
Внутренняя точка области определения функции, в которой производная равна нулю или не существует, называется
критической точкой функции.
Внутренняя точка области определения, в которой
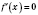
, называется
стационарной точкой функции.
Теорема 2. Если функция
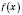
во внутренней точке области определения имеет экстремум, то в этой точке производная
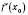
, если она существует, равна нулю.
Теорема 3. Если функция
f является непрерывной в точке
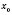
, а
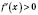
на интервале
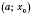
и
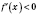
на интервале
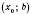
, то точка
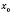
является точкой максимума функции.
Теорема 4. Если функция
f является непрерывной в точке
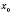
, а
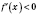
на интервале
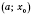
и
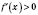
на интервале
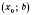
, то точка
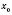
является точкой минимума функции
f.
Теорема 5. Пусть точка
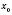
является стационарной для функции
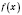
и пусть в этой точке существует производная второго порядка
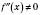
. Тогда, если
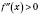
, то
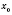
является точкой минимума и, если

, то
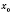
является точкой максимума функции
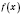
.
Наибольшее и наименьшее значения функции на отрезке
Чтобы найти наибольшее (наименьшее) значение непрерывной функции на отрезке
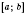
, нужно найти все локальные максимумы (минимумы) и сравнить их со значениями функции, которых она принимает на концах отрезка. Наибольшее (наименьшее) число среди образованной множества и будет наибольшим (наименьшим) значением функции, заданной на отрезке
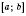
.
Обозначения:
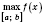
;
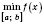
.