Арифметические операции над функциями диференційовними

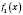
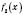
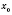
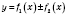
Теорема 1. Если функции и в точке имеют производные, то функция в этой точке также имеет производную, которая равна
.
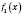
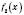
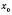
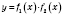
Теорема 2. Если функции и в точке имеют производные, то в этой точке функция также имеет производную, которая равна
.
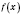
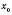
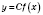
Следствие. Если функция имеет производную в точке , то функция также имеет производную в этой точке, равна .
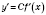
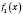
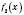
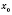
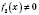
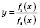
Теорема 3. Если функции и в точке имеют производные и , то функция также имеет производную в точке x:
.
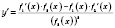
Пусть функция f ставит в соответствие числу x число y, а функция g - числу y число z. Тогда функцию h, которая ставит в соответствие числу x число z, называют составленной функцией.
Обозначения: .
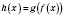
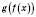
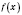
Обратите внимание: область определения функции - это множество таких значений x из области определения функции f, для которых принадлежит области определения функции g.
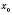
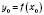
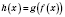
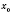
Теорема 4. Если функция f имеет производную в точке , а функция g имеет производную в точке , то составленная функция также имеет производную в точке , причем .
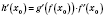
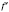
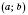
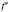
Пусть функция f имеет производную во всех точках промежутка . Эта производная, в свою очередь, является функцией от x. Если функция діференційовна, то ее производную называют второй производнойf и обозначают .
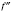
Таким образом, .
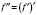
Таким же образом дают определение производной n-го порядка .
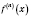