АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел II. УРАВНЕНИЯ И НЕРАВЕНСТВА

§7. РЕШЕНИЕ УРАВНЕНИЙ, СВОДЯЩИХСЯ К КВАДРАТНЫМ.

1. Дробные рациональные уравнения.

При решении дробного рационального уравнения можно использовать различные способы. Рассмотрим два из них.

Первый способ заключается в использовании условия равенства дроби нулю: дробь a/b равна нулю тогда и только тогда, когда а = 0 и b ≠ 0.

Пример 1. Решите уравнение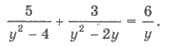

Решения. Разложим на множители знаменатели дробей и перенесем дробь из правой части уравнения в левую

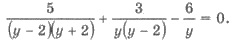
Давайте приведем дроби в левой части уравнения к общему знаменателю.

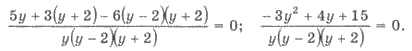
Последнее уравнение равносильно системе:

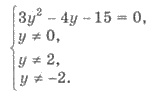
Отсюда получим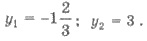

Пример 2. Решите уравнение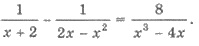

Решения. Разложим на множители знаменатели дробей.

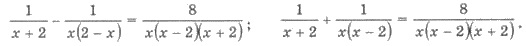
Домножимо обе части уравнения на общий знаменатель дробей - выражение х(х - 2)(х + 2) при условии, что он не равен нулю. Имеем:

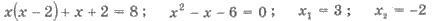
Если х = 3, то х(х - 2)(х + 2) ≠ 0, следовательно, х = 3 - корень исходного уровня. Если же х = -2 , то х(х - 2)(х + 2) = 0, поэтому х = -2 - не является корнем уравнения.

Следовательно, х = 3 - единственный корень начального уровня.