АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел II. УРАВНЕНИЯ И НЕРАВЕНСТВА

§6. ТЕОРЕМА ВИЕТА.

Если х₁ и х₂ - корни квадратного сводного уравнение 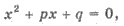то

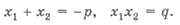
Если х₁ и х₂ - корни квадратного уравнения 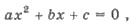то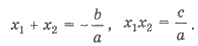

Пример 1. Уравнение 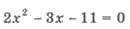имеет положительный дискриминантов, то оно имеет корни х₁ и х₂. По теореме Виета

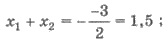
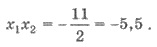
Пример 2. Один из корней уравнения 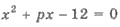равен 2. Найдите p и второй корень.

Решения. По условию х₁ = 2 - корень уравнения 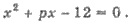Пусть х₂ - второй корень этого уравнения. По теореме Виета 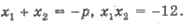Учитывая х₁ = 2 , имеем:

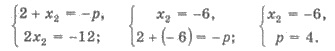
Пример 3. х₁ и х₂ - корни уравнения 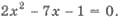Не решая уравнение, найти:

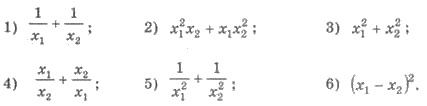
Решения. По теореме Виета 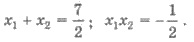Имеем: