Урок 14

Тема. Решение задач

Цель урока: формирование умений учащихся применять признак параллельности прямой и плоскости к решению задач.

Оборудование: стереометрический набор.

Ход урока

И. Проверка домашнего задания

1. Два ученика на откидных досках воспроизводят решения задач № 14, 16. В это время класс выполняет математический диктант.

2. Математический диктант.

Дано изображение куба: вариант 1 - рис. 53, вариант 2 - рис. 54.

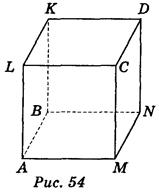
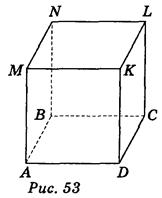
Пользуясь изображением, запишите:

1) прямую, которая параллельна плоскости ВСМ и проходит через точку D; (2 балла)

2) грани куба, которые параллельны прямой CD; (2 балла)

3) плоскость, содержащая прямую ВN и параллельная прямой С,D; (2 балла)

4) плоскость, параллельная прямой С,D и проходит через точку К; (2 балла)

5) плоскости, которые параллельны прямой ВМ; (2 балла)

6) прямые, параллельные плоскости АВМ. (2 балла)

Ответ. Вариант 1.1) D; 2) АВNМ и МNLК; 3) АВN; 4) КМN и АВК; 5) DСК, LСА, КDM; 6) КL, LС, СD, ЕD, КС, DL.

Вариант 2.1) DN; 2) АВКL, АВNМ; 3) АВN; 4) АВК и КLМ; 5) СDК, КCN, КСА; 6) KL, LС, СD, KD, KС, DL.

3. Провести коллективное обсуждение результатов работы на откидных досках, написание математического диктанта.

II. Обобщение и систематизация знаний учащихся

Свойства прямой и плоскости, которые параллельны между собой

Целесообразно рассмотреть такие задачи на доказательство.

1. Докажите, что если плоскость проходит через прямую, которая параллельна второй плоскости, и пересекает эту плоскость, то прямая пересечения параллельна данной прямой.

Решение

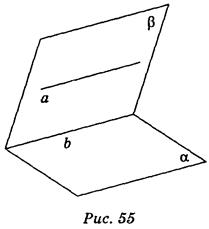
Пусть а || a (рис. 55) и плоскость b проходит через а, b - прямая пересечения плоскостей a и b. Докажем, что а || b. Прямые а и b лежат в одной плоскости b и не пересекаются, потому что в противном случае прямая а пересекала бы плоскость a, что невозможно, поскольку согласно условию а || a. Следовательно, а || b.

2. Докажите, что если через каждую из двух параллельных прямых проведена плоскость, причем эти плоскости пересекаются, то линия пересечения параллельна каждой из данных прямых.

Решение

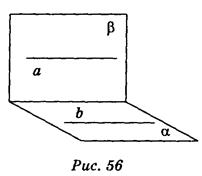
Пусть а || b, прямая а лежит в плоскости a , прямая b лежит в плоскости b, плоскости a и b пересекаются по прямой с (рис. 56). Докажем, что а || с , b || с. Поскольку а || b и прямая b лежит в плоскости b, то а || b и, следовательно, в соответствии с решением задачи 1, а || с. Аналогично, поскольку а || b, а лежит в плоскости a, b || a и, следовательно, b || с. Таким образом, а || с и b || с.

3. Докажите, что если две плоскости пересекаются, параллельные одной и той же прямой, то прямая пересечения этих плоскостей параллельна данной прямой.

Решение

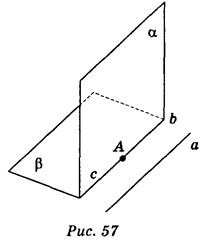
Пусть a и b пересекаются по прямой с, а || a, а || b (рис. 57). Докажем, что а || с. Возьмем на прямой произвольную точку с А и через нее проведем прямую b, параллельную прямой а. Поскольку прямая а || a, а || b, то прямая b лежит как в плоскости a, так и в плоскости b. Следовательно, прямая b - прямая, по которой пересекаются плоскости a и b, поэтому прямая b совпадает с прямой с, следовательно с || а.

III. Закрепление и осмысление знаний учащихся

Решение задач

1. Задача № 13 (1, 4) из учебника (с. 19).

2. Плоскость a и прямая а параллельные одной и той же прямой b. Докажите: если прямая а не лежит в плоскости a, то а || a.

3. Докажите, что все прямые, которые пересекают одну из мимобіжних прямых и параллельных второй, лежат в одной плоскости.

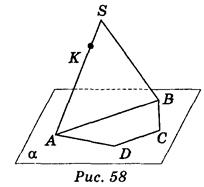
4. Трапеция АВСD (АВ || СD) лежит в плоскости a (рис. 58), АВ = 12 см. Вне плоскости a взяли точку S и на отрезке SА отметили точку К такую, что АК:КS=3:1. Постройте точку Х - точку пересечения плоскости DКС и отрезка SВ и найдите длину отрезка КВ.

5. Задача № 17 из учебника (с. 19).

IV. Домашнее задание

§2, п. 9; задачи№ 13 (2, 3), 22 (с. 19-20).

V. Подведение итога урока

Вопрос к классу

1) Сформулируйте признак параллельности прямой и плоскости.

2) Сформулируйте утверждение, обратное признаки параллельности прямой и плоскости. Правильное ли оно?

3) Завершите утверждение.

а) Если плоскость проходит через прямую, которая параллельна второй плоскости, и пересекает эту плоскость, то прямая пересечения ... .

б) Если через каждую из двух параллельных прямых провести плоскости, которые пересекаются, то их линия пересечения ... .

в) Если две плоскости, которые пересекаются, параллельные одной и той же прямой, то прямая пересечения этих плоскостей ... .