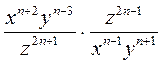Урок № 14
Тема. Умножение дробей. Подъем дроби в степень
Цель: закрепить знания учащихся по способам преобразования произведения и степени рационального дроби рациональная дробь; отработать умение использовать приобретенные знания для выполнения названных преобразований рациональных выражений.
Тип урока: применение знаний, умений и навыков.
Наглядность и оборудование: опорный конспект «Умножение и деление дробей. Подъем дроби в степень».
Ход урока
I. Организационный этап
II. Проверка домашнего задания
Учитель проверяет выполнение работы у учащихся, требующих дополнительного педагогического внимания (собрать их тетради для проверки и при необходимости раздать материалы для проведения коррекционной работы).
Фронтально можно провести работу в форме «Найди ошибку» - предложить ученикам найти в решении упражнений домашнего задания «ошибки» (которые учитель умышленно допустил в предложенном учащимся варианте выполнения домашнего задания). Этот вид работы можно провести как устно, так и в форме письменной самостоятельной работы. В последнем случае - результаты выполнения работы следует сразу же проверить (например, во время работы в парах) и скорректировать полученные ответы; учеников, которые справятся с заданием без ошибок, следует поощрить соответствующими оценками.
III. Формулировка цели и задач урока, мотивация учебной деятельности учащихся
Результаты проверки выполнения домашнего задания и (или) самостоятельных упражнений в начале урока, а также последующее обсуждение допущенных ошибок дают возможность учащимся осознать необходимость продолжения работы по формированию навыков применения изученных на предыдущих двух уроках алгоритмов преобразований:
· произведения рациональных дробей;
· произведения рационального дроби на целое выражение;
· степень рационального дроби.
Отработка навыков применения учащимися названных алгоритмов и совершенствование этих навыков (если они сформированы на предыдущих уроках) составляет основную дидактическую цель урока.
IV. Актуализация опорных знаний и умений
Согласно цели урока перед развязыванием письменных упражнений следует активизировать знания и умения учащихся: выполнение арифметических действий с рациональными числами и применения при нем изученных ранее свойств этих действий; выполнение действия умножения целого выражения на рациональный дробь и возведение дроби в степень; преобразования рациональных дробей, изученных на предыдущих уроках.
Выполнение устных упражнений
1. Вычислите: 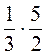 ;
; 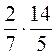 ;
; 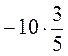 ;
; 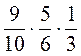 ;
; 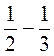 ;
; 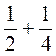 ;
; 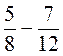 .
.
2. Представьте в виде степени с основанием т выражения: m ∙ m ∙ m3; m5 : m : m2; m5 : (m2)2; 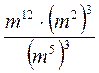 ; (m ∙ m5)4.
; (m ∙ m5)4.
3. Найдите значения выражений 3а; 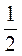 а; 1 - а;
а; 1 - а; 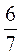 а; а3; (-а)3; (2а)2; 2а2 при а =
а; а3; (-а)3; (2а)2; 2а2 при а = 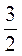 .
.
4. Представьте в виде дроби выражение: 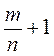 ;
; 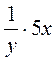 ;
; 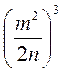 ;
; 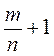 ;
; 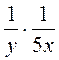 ;
; 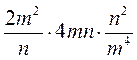 ;
; 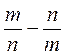 ;
; 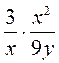 ;
; 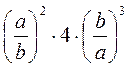 ;
; 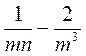 .
.
V. Совершенствование умений и павичок
Выполнение устных упражнений
1. Разложите выражение на множители:
а) mn - m; б) 3m2 - 6m; в) х3 - 4х; г) m3 - n2m; д) а3 - k3; е) х - у + х2 - у2; ж) 4х2 - 16х + 16; с*) (m + n)2 - 1; ы*) (m + n)2 - 2(m + n) + 1.
2. Даны выражения: bx + b2; b + x; x. Используя каждый из них по одному разу, назовите (запишите) две дроби, чтобы их произведение равен: а) 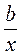 ; б) bх; в)
; б) bх; в) 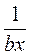 ; г)
; г) 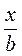 .
.
3. Какого значения (равного или противоположного) приобретают при одном и том же значении переменной выражения:
а) -m и -(-m); б) m - 1 и 1 - т; в) 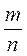 и
и 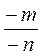 ; г)
; г) 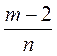 и
и 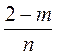 ; д)
; д)  и
и 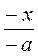 ; е)
; е) 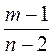 и
и 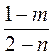 ?
?
Выполнение письменных упражнений
@ Содержание упражнений, вынесенных на текущий урок, так же как и на предыдущих уроках, направленный на формирование навыков быстрого и безошибочного преобразования произведения рациональных дробей, произведения рациональной дроби и целого выражения, степени рационального дроби, а также преобразования «комбинированных» выражений на рациональный дробь. Этого можно добиться за счет выполнения достаточного количества упражнений различного уровня сложности. Для того чтобы оживить эту однообразную работу, учитель может организовать ее проведение в нестандартном виде, например в форме математической эстафеты, математического боя или подготовить задания на карточках-подсказках.
Так же как и на предыдущем уроке, выполнение преобразований рациональных выражений сопровождается широким использованием формул сокращенного умножения, правила изменения знака дроби, различных способов разложения многочленов на множители. Во время устной работы на уроках полезно предлагать учащимся упражнения на повторение этих моментов.
Также не следует забывать о необходимости дальнейшего формирования палочек выполнения действий сложения и вычитания рациональных дробей. Эта работа проводится через систему устных и повторювальних упражнений. Не следует забывать и о проведение систематической работы с учащимися, которые имеют склонность к изучению математики, и предлагать их внимания задания высокого уровня сложности и конкурсные задания по теме, которая изучается.
Дня реализации дидактической цели на этом уроке следует решить задачи следующего содержания.
1. Умножение рациональных дробей (в разных ситуациях).
1) Выполните умножение:
а) 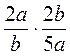 ; б)
; б) 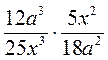 ; в)
; в) 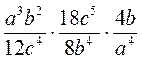 ; г)
; г) 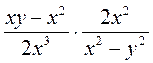 ; д)
; д) 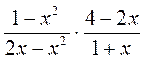 ; е)
; е) 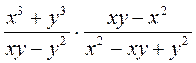 .
.
2) Представьте в виде дроби:
а) 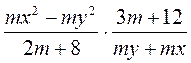 ; б)
; б) 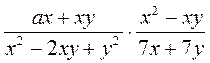 ; в)
; в) 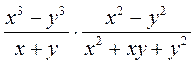 ; г)
; г) 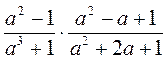 ; д)
; д) 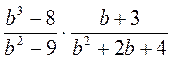 ; е)
; е) 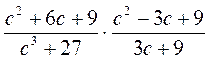 .
.
3) Упростите выражение:
а) 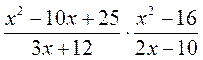 ; б)
; б) 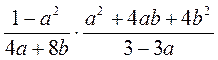 ; в)
; в) 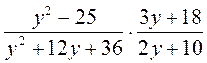 ; г)
; г) 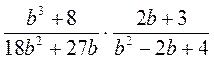 .
.
2. Подъем рационального дроби в степень. Возведите в степень:
а) 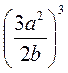 ; б)
; б) 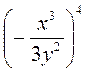 ; в)
; в) 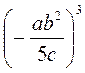 ; г)
; г) 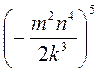 .
.
3. Упрощение выражений (предусматривает выполнение преобразований рациональных выражений, содержащих несколько арифметических действий одной ступени или более чем два множители).
1) От пристани А до пристани В по течению реки одновременно отплыли катер и плот. Когда через 1,5 ч катер прибыл к пристани В, плоту оставалось проплыть до В еще 27 км. Не задерживаясь на пристани В, катер отправился в обратный путь. Через какое время после отправления от пристани В катер встретит плот? Какова скорость катера в стоячей воде?
2) Упростите выражение: а) 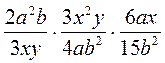 ; б)
; б) 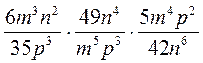 .
.
VII. Итоги урока
Самостоятельная работа № 3
Вариант 1 |
Вариант 2 |
Представьте в виде дроби выражение: |
а) 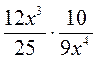 ; б) ; б) 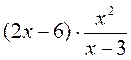 ; ;
в) 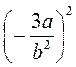 ; г) ; г) 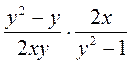 ; ;
д) 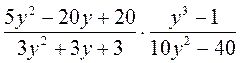 ; ;
есть*) 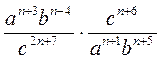
(n - натуральное число, п > 4) |
а) 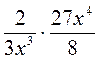 ; б) ; б) 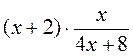 ; ;
в) 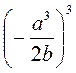 ; г) ; г) 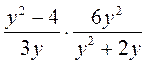 ; ;
д) 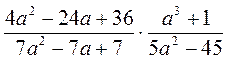 ; ;
есть*) 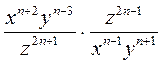
(n - натуральное число, п > 3) |
VIII. Домашнее задание
1. Повторить алгоритмы выполнения действий сложения и вычитания, а также умножения рациональных дробей и особые случаи их применения.
2. Выполнить упражнения на применение изученных алгоритмов.
3. Повторить: содержание понятия «взаимно обратные числа» и алгоритм нахождения числа, обратного к данному; правило деления обыкновенных дробей и особые случаи его применения (деление обыкновенной дроби на целое число, и наоборот; деление смешанных чисел и т, д.).
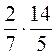 ;
; 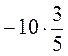 ;
; 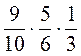 ;
; 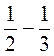 ;
; 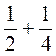 ;
; 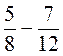 .
.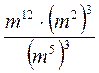 ; (
; (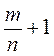 ;
; 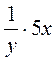 ;
; 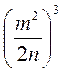 ;
; 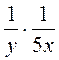 ;
; 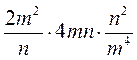 ;
; 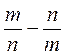 ;
; 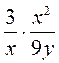 ;
; 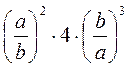 ;
; 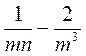 .
.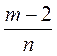 и
и 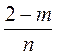 ; д)
; д) 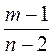 и
и 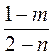 ?
?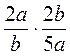 ; б)
; б) 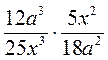 ; в)
; в) 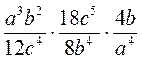 ; г)
; г) 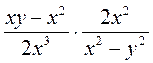 ; д)
; д) 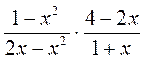 ; е)
; е) 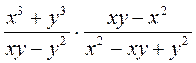
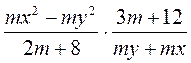 ; б)
; б) 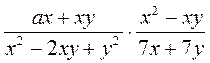
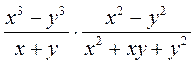 ; г)
; г) 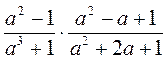 ; д)
; д) 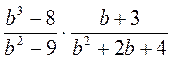 ; е)
; е) 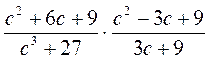 .
.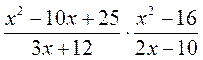 ; б)
; б) 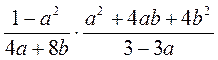 ; в)
; в) 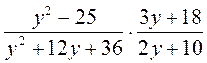 ; г)
; г) 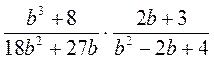 .
.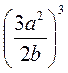 ; б)
; б) 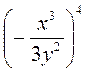 ; в)
; в) 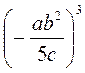 ; г)
; г) 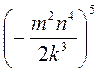 .
.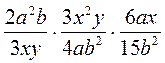 ; б)
; б) 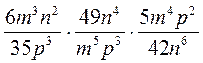 .
.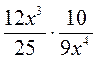 ; б)
; б) 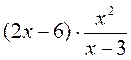 ;
;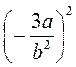 ; г)
; г) 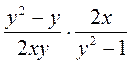 ;
;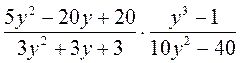 ;
;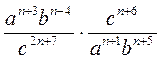
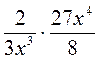 ; б)
; б) 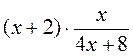 ;
;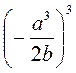 ; г)
; г) 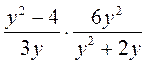 ;
;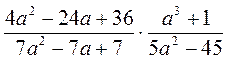 ;
;