Урок № 13
Тема. Умножение дробей. Подъем дроби в степень
Цель: добиться усвоения учащимися схемы действий во время умножения рационального дроби на целое выражение, а также алгоритма подъема рационального дроби в натуральную степень и выполнения совместных действий подъема дроби в степень и умножения рациональных дробей; сформировать умение сознательно воспроизводить изученные схемы, а также выполнять действия по этим схемам при выполнении соответствующих преобразований рациональных выражений.
Тип урока: применение знаний, умений и навыков.
Наглядность и оборудование: опорный конспект «Умножение и деление рациональных дробей».
Ход урока
I. Организационный этап
II. Проверка домашнего задания
Проверку выполнения упражнений домашнего задания можно осуществить по образцу.
Для учеников, которые хорошо усвоили материал предыдущего урока, можно предложить индивидуальные задания (содержания, аналогичного упражнений домашнего задания или с элементами нестандартности).
III. Формулировка темы и задач урока
При условии осознания учащимися существование определенной аналогии между алгоритмами выполнения арифметических действий с обыкновенными и рациональными дробями, во время проверки последней части домашнего задания (см. 4 пункт домашнего задания предыдущего урока) учащиеся должны предусмотреть учебную ситуацию, которая будет рассмотрена на текущем уроке: случай умножения рационального дроби на целое выражение, а также умножение рациональных выражений с применением свойств умножения.
Названы «проблемные ситуации» (противоречия между приобретенными ранее знаниями и существующей ситуацией) должны быть развязаны. Это и является основной дидактической целью урока.
IV. Актуализация опорных знаний и умений
@ Согласно цели урока перед изучением вопроса о умножения рационального дроби на целое выражение подъем рационального дроби в степень следует активизировать знания и умения учащихся относительно способа представления целого числа (выражения) в виде дроби с заданным знаменателем, выполнение действия умножения целого числа на обыкновенную дробь, основного свойства степени и ее последствий (особенно подъем дроби и произведения в степень), а также преобразований рациональных дробей, изученных на предыдущих уроках.
Выполнение устных упражнений
1. Вычислите: 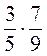 ;
; 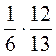 ;
; 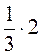 ;
; 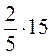 ;
; 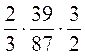 ;
; 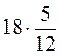 ;
; 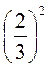 ;
; 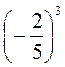 .
.
2. Разложите на множители выражение:
а) mx - m; б) m2 + n2 - 2mn; в) х - у + 2х - 2у; г) m2 - n2; д) 14n2 - 14; е) 2m3 - 16.
3. Представьте выражения в виде дроби:
а) 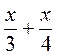 ; б)
; б) 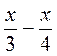 ; в)
; в) 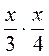 ; г)
; г) 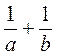 ; д)
; д) 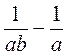 ; е)
; е) 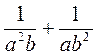 ; ж)
; ж) 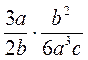 ; з)
; з) 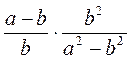 ; и)
; и) 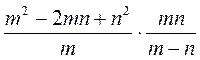 .
.
4. Упростите выражение: (2х)2; (-3х)2; (х2)3; (3х2)3; а2 - 2ab)3.
V. Усвоение знаний
План изучения нового материала
1. Алгоритм умножения рационального дроби на целое выражение.
2. Правило подъема дроби в степень (с доводкой). Алгоритм подъема дроби в степень.
3. Алгоритм выполнения действий в более сложных выражениях, содержащих несколько действий.
4. Примеры применения составленных алгоритмов.
@ Правило выполнения умножения рационального дроби на целое выражение имеет такую же форму, как и правило умножения обыкновенной дроби на целое число: оно выражается формулой 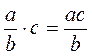 (это правило умножения дробей ученики изучали по учебнику «Математика, 5 класс», авторы: Мерзляк А. Г. и другие). Согласно этой формуле ученики должны составить схему действий во время выполнения такого преобразования в общем случае.
(это правило умножения дробей ученики изучали по учебнику «Математика, 5 класс», авторы: Мерзляк А. Г. и другие). Согласно этой формуле ученики должны составить схему действий во время выполнения такого преобразования в общем случае.
Доказательство тождества 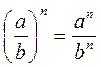 опирается на определение степени с натуральным показателем и на правило умножения рациональных дробей. Поэтому это доведение ученики могут провести самостоятельно, а также самостоятельно составить ориентировочную схему выполнения этого действия.
опирается на определение степени с натуральным показателем и на правило умножения рациональных дробей. Поэтому это доведение ученики могут провести самостоятельно, а также самостоятельно составить ориентировочную схему выполнения этого действия.
Что касается более сложных случаев (в выражении содержится сразу два и более действий), то учащимся следует напомнить о существовании понятия арифметических действий и последовательность выполнения действий различной степени (от самого старшего до самого низкого степеней при условии существования или отсутствия скобки, изменяющие порядок выполнения действий).
Закончить изучение материала урока следует приведением соответствующих примеров на применение изученных схем действий (с одновременным комментарием).
VI. Формирование умений
Выполнение устных упражнений
1. Прокомментируйте выполнения действий в выражении:
а) 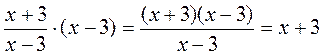 ;
;
б) 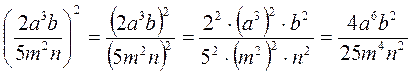 .
.
2. Представьте выражения в виде дроби: а) 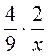 ; б)
; б) 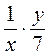 ; в)
; в) 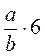 ; г)
; г) 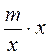 ; д)
; д) 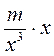 ; е)
; е) 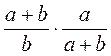 ; ж)
; ж) 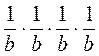 ; з)
; з) 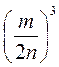 ; и)
; и) 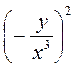 .
.
3. Определите последовательность выполнения действий: а) 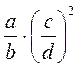 ; б)
; б) 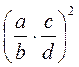 ; в)
; в) 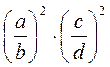 ; г)
; г) 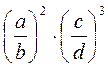 .
.
Выполнение письменных упражнений
Для реализации дидактической цели урока следует решить задачи следующего содержания.
1. Умножение рациональных дробей на целое выражение (разной степени сложности).
1) Представьте в виде дроби: 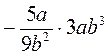 .
.
2) Выполните умножение: 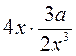 .
.
3) Преобразуйте в дробь выражение: а) 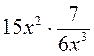 ; б)
; б) 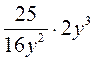 ; в)
; в) 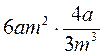 ; г)
; г) 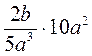 .
.
4) Представьте в виде дроби: а) 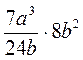 ; б)
; б) 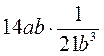 .
.
5) Выполните умножение: а) 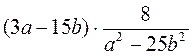 ; б)
; б) 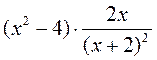 ; в)
; в) 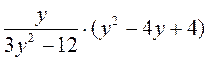 ; г)
; г) 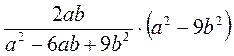 .
.
2. Подъем рационального дроби в степень.
1) Возведите в степень: а) 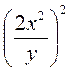 ; б)
; б) 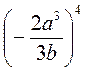 ; в)
; в) 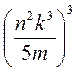 ; г)
; г) 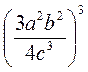 .
.
2) Возведите в степень: а) 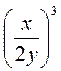 ; б)
; б) 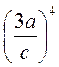 ; в)
; в) 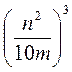 ; г)
; г) 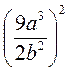 .
.
3) Возведите в степень: а) 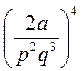 ; б)
; б) 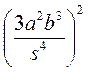 ; в)
; в) 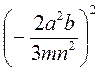 ; г)
; г) 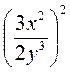 .
.
3. Упрощение выражений (предусматривает выполнение преобразований рациональных выражений, содержащих несколько арифметических действий одной ступени, или больше, чем два множители).
1) Выполните умножение:
а) 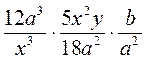 ; б)
; б) 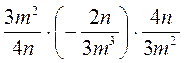 ; в)
; в) 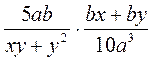 ; г)
; г) 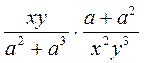 ; д)
; д) 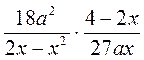 ; е)
; е) 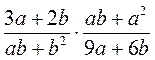 .
.
2) Упростите выражение 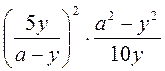 .
.
3) Упростите выражение: а) 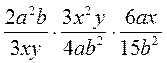 ; б)
; б) 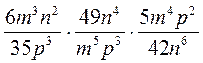 .
.
4. Вычисление значений выражений с предварительным упрощением его по изученным ранее и на данном уроке схемами.
1) Найдите значение выражения 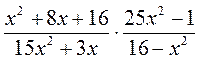 при х = -1; х = 5; х =
при х = -1; х = 5; х = 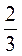 .
.
2) Найдите значение выражения:
а) 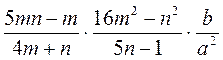 , если m =
, если m = 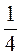 , n = -3;
, n = -3;
б) 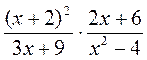 , если х = 0,5; -1,5.
, если х = 0,5; -1,5.
5. Выполнение упражнений на повторение: преобразовать сумму или разность рациональных дробей на рациональный дробь.
Упростите выражение:
а) 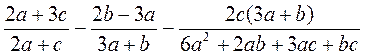 ;
;
б) 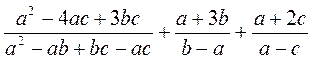 .
.
6. Выполнение логических упражнений и заданий повышенного уровня сложности для учащихся, имеющих достаточный и высокий уровни знаний.
1) Найдите значение выражения 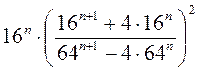 при n = 74; n = 1000.
при n = 74; n = 1000.
2) Упростите выражение: а) 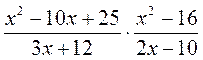 ; б)
; б) 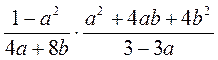 ; в)
; в) 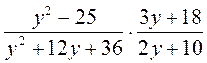 ; г)
; г) 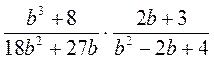 .
.
3) Исключите лишнюю пару чисел:
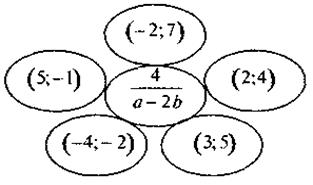
@ Упражнения, предлагаемые для решения на урок, должны быть направлены на формирование навыков быстрого и безошибочного преобразования произведения рационального дроби на целое выражение в рациональный дробь, степень рационального дроби в рациональный дробь, а также преобразования «комбинированных» выражений в рациональный дробь. Этого можно добиться за счет достаточно большого количества упражнений различного уровня сложности (см. выше).
Так же как и на предыдущем уроке, выполнение преобразований рациональных выражений сопровождается широким использованием формул сокращенного умножения, правила изменения знака дроби, различных способов разложения многочленов на множители. Во время устной работы на уроках полезно предлагать учащимся упражнения на повторение этих моментов.
Также не следует забывать о необходимости дальнейшей отработки навыков выполнения умножения рациональных дробей и действий сложения и вычитания рациональных дробей. Эта работа проводится через систему устных и повторювальних упражнений.
VII. Итоги урока
В любом из случаев правильно выполнено действие с рациональными дробями?
а) 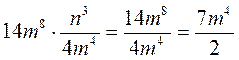 ; б)
; б) 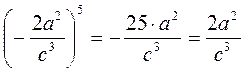 ; в)
; в) 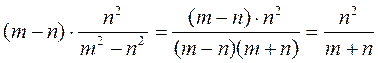 ; г)
; г) 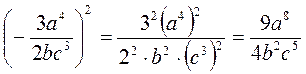 .
.
VIII. Домашнее задание
1. Изучить алгоритмы выполнения действий, составленных и обработанных на уроке.
2. Решить задачи на формирование навыков использования изученных алгоритмов.
3. На повторение: упражнения на выполнение действий с рациональными дробями.