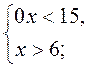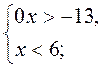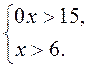УРОК № 14
Тема. Решение систем и совокупностей) линейных неравенств с одной переменной
Цель урока: закрепление учащимися знаний содержания понятий: неравенство с одной переменной, решение неравенства с одной переменной и что значит решить неравенство с одной переменной; система неравенств с одной переменной, решение системы неравенств с одной переменной и что значит решить систему неравенств с одной переменной; совокупность неравенств с одной переменной, решение совокупности неравенств с одной переменной и что значит решить совокупность неравенств с одной переменной, а также закрепление знаний учащихся о схемы решения линейных неравенств с одной переменной, их систем и совокупностей. Дополнение знаний учащихся схемами решения простейших неравенств с модулем (с использованием геометрического смысла модуля), а также примерами задач на составление и решение систем неравенств с одной переменной (в частности на нахождение ОДЗ выражения). Выработать у учащихся умения: воспроизводить содержание изученных понятий и использовать их для решения практических задач.
Тип урока: совершенствование умений, отработка навыков.
Наглядность и оборудование: опорный конспект № 11.
Ход урока
I. Организационный этап
Учитель проверяет готовность учащихся к уроку, настраивает их на работу.
II. Проверка домашнего задания
Учитель проверяет выполнение работы у учащихся, требующих дополнительного педагогического внимания (собирает их тетради для проверки и при необходимости раздает материалы для проведения коррекционной работы).
Фронтально можно провести в форме игры «Найди ошибку» - предложить ученикам найти в решении упражнений домашнего задания «ошибки» (которые учитель умышленно сделал в предложенном учащимся варианте выполнения домашнего задания). Этот вид работы можно провести как в устной форме, так и в форме письменной самостоятельной работы. В последнем случае результаты выполнения работы, следует сразу же проверить (например, в нарах) и скорректировать; учащихся, что справятся с заданием без ошибок, следует поощрить соответствующими оценками.
III. Формулировка цели и задач урока.
Мотивация учебной деятельности учащихся
Результаты (то есть допущенные учениками ошибки) выполнение домашнего задания и/или самостоятельных упражнений в начале урока, а также последующее обсуждение допущенных ошибок дают возможность учащимся осознать необходимость продолжения работы по отработке навыков применения изученных на предыдущих трех уроках алгоритмов. Кроме того, на этом этапе урока будут уместными слова учителя о том, что решение систем и совокупностей неравенств с одной переменной является средством решения некоторых видов неравенств; о некоторых из таких неравенств речь будет идти на данном уроке.
Таким образом, совершенствование навыков решения неравенств с одной переменной и их систем и совокупностей вместе с изучением сферы их практического применения составляет основную дидактическую цель урока.
IV. Актуализация опорных знаний и умений учащихся
Устные упражнения
1. Решите неравенство:
1) 3х > 6;
2) -х > -5;
3) -х 0;
4) 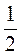 х > -2;
х > -2;
5) 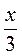 -4;
-4;
6) 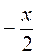 > 1,5.
> 1,5.
2. Решите систему неравенств:
1) 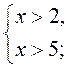 2)
2) 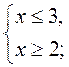 3)
3) 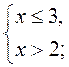 4)
4) 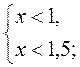 5)
5) 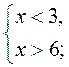 6)
6) 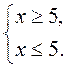
3. Назовите несколько чисел, которые удовлетворяют условию:
1) | x | = 2; 2) | x | > 2; 3) | х | 2.
V. Дополнение знаний
План изучения нового материала
1. Решение неравенств вида | х | а.
2. Решение неравенств вида | х | > а.
3. Примеры задач на составление и решение систем неравенств с одной переменной.
Методический комментарий
Изложение вопроса о решения простейших неравенств с модулем ведется традиционно основывается на геометрическом смысле модуля (модуль числа - это расстояние от начала отсчета на координатной прямой до данной точки). Поэтому для лучшего понимания учениками схем решения этих неравенств перед их изучением необходимо провести соответствующую работу с повторения знаний и умений учащихся по определению модуля числа и некоторых свойств модуля, а также по решению линейных неравенств с одной переменной и их систем и совокупностей (см. устные упражнения выше).
Также традиционно рассматривается вопрос о применении систем уравнений для решения стандартной задачи на нахождение ОДЗ выражения, содержащего переменную под знаком арифметического квадратного корня.
Опорный конспект № 11
Простейшие неравенства с модулем |
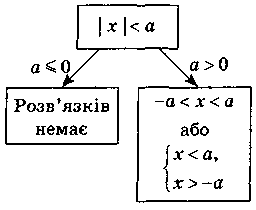
|
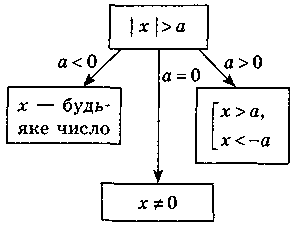
|
Например:
|x - 1| 3;
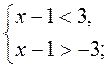 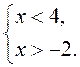
x  (-2; 4). (-2; 4). |
Например:
|x - 1| > 3;
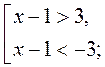 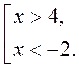
x  (-∞; -2) (-∞; -2) 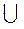 (4; +∞). (4; +∞). |
Пример 1. Определим, при каких значениях переменной имеет смысл выражение
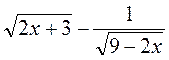 . .
Решение |
Выражение 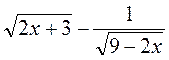 имеет смысл, когда підкореневі выражения неотрицательны и знаменатель не равен 0, то есть выполняется система: имеет смысл, когда підкореневі выражения неотрицательны и знаменатель не равен 0, то есть выполняется система: |
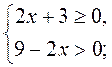 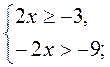 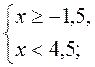 х є [-1,5; 4,5). х є [-1,5; 4,5).
|
Ответ: [-1,5; 4,5). |
Пример 2. Решим неравенство | 7х + 8 | 2. |
Решение |
Данное неравенство равносильно системе: |
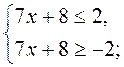 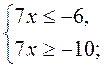 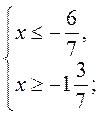 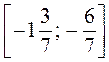 . .
Ответ: 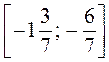 . . |
VI. Отработка навыков. Совершенствование умений
Устные упражнения
1. Каждое из неравенств заменить равносильной системе или совокупности неравенств:
1) |x| > 3;
2) |x| 3;
3) |х - 2 | > 2;
4) |x - 3| 1.
2. Решите систему неравенств:
1) 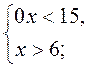 2)
2) 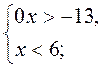 3)
3) 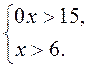
Письменные упражнения
Методический комментарий
Содержание упражнений, вынесенных на текущий урок, так же, как и на предыдущих уроках, имеет направление на выработку навыков безошибочного выполнения следующих действий:
1) равносильные преобразования неравенств с одной переменной;
2) решение линейных неравенств с одной переменной;
3) решение систем и совокупностей линейных неравенств с одной переменной;
4) решение неравенств вида | x | а путем решения систем линейных неравенств с одной переменной;
5) решение неравенств вида | х | > а путем решения совокупности линейных неравенств с одной переменной.
Этого можно добиться за счет достаточно большого количества упражнений различного уровня сложности. Для того чтобы оживить эту однообразную работу, учитель может организовать ее проведение в нестандартном виде, например, в форме математической эстафеты, математического боя, или подготовить задания на карточках-подсказках.
Во время устной работы на уроках полезно предлагать учащимся упражнения на повторение этих моментов.
VII. Итоги урока
Ученики выполняют самостоятельную работу № 4 в тетради для самостоятельных и контрольных работ [8].
VIII. Домашнее задание
1. Изучить схемы решения неравенств вида | x | а, | х | > а.
2. Выполнить упражнения на применение изученных схем.
3. Повторить: содержание основных понятий темы 1 и схем действий, изученных в этой теме, а также составить общую схему, отражающую логическую связь между вопросами темы; решить упражнения на применение этих теоретических положений (см. содержание упражнений классной работы).
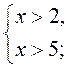
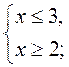
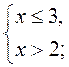
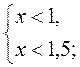
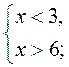
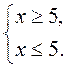


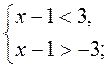
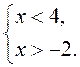
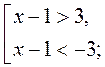
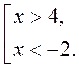
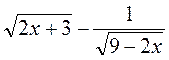 .
. 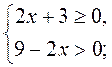
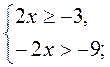
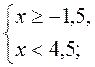
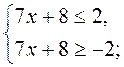
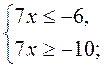
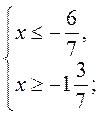
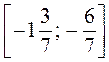 .
.