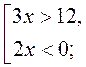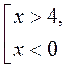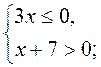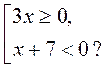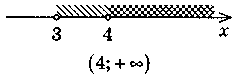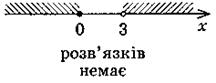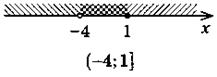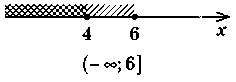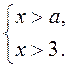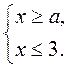|
Методический комментарий Если на предыдущих уроках у учащихся сформировались четкие представления о содержании понятий: система неравенств с одной переменной, совокупность неравенств с одной переменной, пересечение и объединение числовых промежутков, решение неравенства с одной переменной, решение системы и совокупности неравенств с одной переменной, а также устойчивые навыки решения линейных неравенств с одной переменной и равносильных преобразований неравенств к виду линейных, то при изучении материала данного урока ученики обычно не имеют трудностей. Поэтому перед изучением содержания нового материала урока уместно будет провести актуализацию основных необходимых для этого знаний и умений, которых учащиеся приобрели в течение предыдущих уроков (см. устные упражнения выше). Схемы, которые предлагаются к обработке (см. план), являются стандартными и полностью соответствуют представлениям учащихся о содержании понятий «что значит решить систему неравенств с одной переменной» и «что значит решить совокупность неравенств с одной переменной» (поэтому можно предложить составить эти схемы самим учащимся).' Однако примеры на применение составленных схем уместно подобрать таким образом, чтобы учащиеся увидели как можно больше разных случаев решений этих систем или совокупностей (например, когда одно из неравенств не имеет решений или когда одно из неравенств имеет решением всю числовую прямую и т. д.). Также (если позволяет время и уровень активности интеллектуальной деятельности учащихся на данном уроке можно рассмотреть «особые случаи» систем линейных неравенств с одной переменной, которые можно решать без помощи числовой прямой по правилам «больше большего» (для систем неравенств вида х > а, х > b) и «меньше меньшего» (для систем неравенств вида х а, х b). В конце беседы о применение изученных схем следует обсудить вопрос о применении решения систем неравенств с одной переменной для решения двойных неравенств (особенно в случаях, когда иным способом, то есть через применение свойств числовых неравенств, это сделать бывает весьма проблематично).
VI. Формирование умений Устные упражнения 1. Есть числа: -4; 0; 5 - развязками: 1) системы 2. На рисунках обозначены множества решений неравенств системы. Является ли правильным запись множества решений системы?
Письменные упражнения Упражнения, предлагаемые к решению на уроке, должны воспроизводить описанные в теоретической части урока ситуации, а именно предусматривать закрепление знаний и выработку умений применять: 1) схему решения систем неравенств с одним неизвестным, сводящиеся к линейным неровностей; 2) схему решения совокупностей неравенств с одним неизвестным, сводящиеся к линейным неровностей; а также дальнейшее совершенствование умений учащихся выполнять равносильные преобразования неравенств с одной переменной и решение линейных неравенств с одной переменной.
Методический комментарий Упражнения, которые следует решить на уроке, должны быть направлены на выработку навыков быстрого, последовательного и безошибочного выполнения действий: а) решения каждого неравенства системы (совокупности); б) нахождение сечения (объединения) найденных промежутков. При этом учителю следует напомнить ученикам, что координатную прямую ученики используют для своего удобства, поэтому рисунок играет вспомогательную роль; это означает, что важным в рисунке есть только правильное изображение последовательности расположения чисел на прямой. После приобретения определенного опыта решения систем неравенств некоторые ученики осознают, что довольно часто решение системы неравенств можно находить и без рисунка, поэтому от таких учеников не следует требовать обязательного выполнения рисунков. Для закрепления всех контрольных моментов, выразившихся в примерах, которые учитель наведет при объяснении нового материала, следует подобрать соответствующие по содержанию тренировочные упражнения.
VII. Итоги урока Контрольные вопросы 1. Что значит «решить систему неравенств»? Опишите действия, которые надо выполнить, чтобы получить решение системы неравенств. 2. Дана система При которых а решением системы является промежуток: 1) (3; +∞); 2) (4; +∞); 3) (3; 4)? 3. Дана система:
VIII. Домашнее задание 1. Изучить алгоритмы выполнения действий, составленных и обработанных на уроке. 2. Решить задачи на формирование навыков использования изученных алгоритмов. 3. Повторить определение и геометрический смысл модуля числа.
|
|
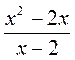
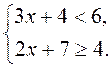
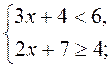
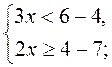
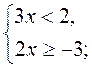
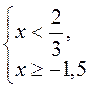
 Ответ: х
Ответ: х