Метод интервалов

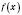
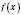
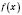
Итак, пусть функция непрерывна на интервале И и превращается в 0 в скінченній количества точек этого интервала. Тогда интервал И разбивается этими точками на интервалы, в каждом из которых сохраняет неизменный знак. Чтобы определить этот знак, достаточно вычислить значения в любой точке каждого такого интервала.
Пример
Решить неравенство
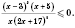
Рассмотрим функцию .
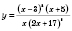
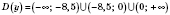
(см. рисунок):

Найдем нули функции :
, .
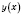
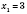
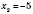
Эти точки делят область определения функции на интервалы, в каждом из которых функция сохраняет постоянный знак (см. рисунок):

.
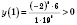
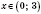
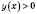
Итак, для получили (ставим на рисунке знак «+» над этим интервалом).
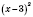
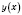
Обратите внимание: в условии показатель степени - четное число. Это означает, что знаки по разные стороны от числа 3 одинаковые.
Остальные показатели степени - числа нечетные. Поэтому, переходя через точки 0; -5; -8,5, знаки меняем на противоположные.
Выбираем промежутки, над которыми стоит знак «-». Неравенство нестрогая, поэтому число -5 тоже является решением.
Ответ: .
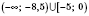