Основные свойства непрерывных функций

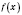
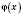
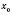
Теорема 1. Если функции и являются непрерывными в точке , то в этой точке будут непрерывными и функции , .
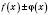
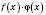
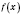
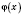
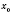
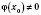
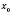
Теорема 2. Если и являются непрерывными в точке и , то в точке является непрерывной также и функция .
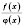
Обратите внимание: все дробно-рациональные функции и основные тригонометрические функции являются непрерывными на любом промежутке, в каждой точке которого они определены. График непрерывной функции на таком промежутке является непрерывной линией.
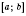
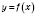
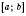
Теорема 3. Пусть функция непрерывна на промежутке и принимает на его концах значения разных знаков. Тогда она обращается в нуль хотя бы в одной точке этого промежутка. Если функция является монотонной на , то она превращается в 0 только один раз.
Последствия
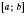
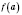
1) Если функция непрерывна на промежутке , то она достает на этом промежутке любое значение M, которое расположено между и .
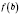
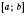
2) Если функция непрерывна на промежутке и не превращается в нуль внутри этого проміжка, то она имеет один и тот же знак во всех внутренних точках промежутка.
Эти свойства позволяют обосновать метод интервалов, который широко применяется для решения неравенств.