Модуль числа - это расстояние от 0 до точки, соответствующей этому числу на координатной прямой, измеренная в единичных отрезках.
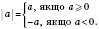
Следовательно,
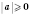
для всех значений
a.
Свойства модуля
1.
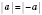
.
2. Если
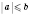
, то
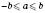
.
3. Если
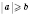
, то
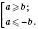
4. Модуль суммы конечного числа действительных чисел не превышает суммы модулей этих чисел:
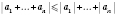
.
5. Модуль разности не меньше разность модулей этих чисел:
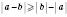
.
6. Модуль произведения конечного числа сомножителей
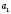
, ...,
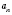
равна произведению модулей этих сомножителей:
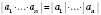
.
7. Модуль частицы равен частному от деления модуля делимого на модуль делителя:
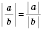
, если
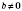
.
Примеры решения уравнений и неравенств, содержащих знак модуля
1)
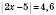
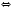
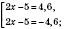
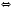
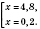 Ответ
Ответ:
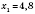
,
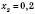
.
2)
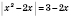
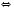
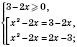
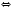
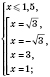
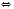
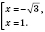
Надо учитывать, что модуль любого числа есть число неотъемлемым, следовательно, корни
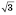
и 3 являются посторонними.
Ответ:
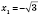
,
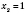
.
3)

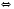
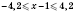
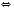
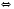
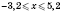
.
Ответ:
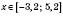
.
4)

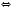
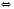
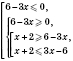
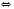
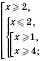
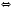
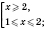
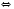
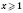
.
Ответ:
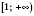
.
Составляя первую совокупность, мы учли, что модуль любого числа есть число неотрицательное. Из этого следует, что при тех значениях
x, когда правая часть является числом недодатним, неравенство всегда выполняется.
5) Очень полезным в решении задач с модулем является способ разделения координатной прямой на такие интервалы, что в них можно определить знак підмодульного выражения и раскрыть знак модуля.
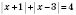
.
Найдем, при каких значениях
х підмодульні выражения превращаются в ноль:
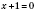
;
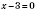
;
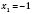
.
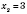
.
Итак, разобьем числовую прямую на три интервала и будем решать уравнение на каждом из них отдельно (см. рисунок).
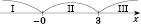
Чтобы определить, какой знак имеет на определенном интервале каждый из підмодульних выражений, достаточно подставить в него вместо
х любое число из этого интервала.
И.
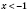
.
Возьмем, например,
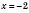
, тогда
,
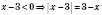
.
Итак, имеем:
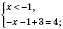
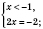
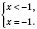
На этом интервале решений не имеет.
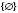
.
II.
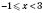
.
Берем
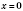
,
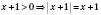
;
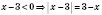
.
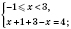
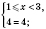
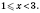
III.
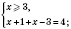
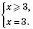
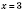
.
Объединяем развязки, полученные на всех трех интервалах (I, II и III).
Ответ:
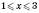
.