Логарифмические неравенства
Решая логарифмические неравенства, опираются на такие утверждения.
1. Если
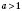
, то неравенство
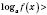
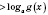
равносильно двойному неравенству
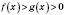
.
Это утверждение можно записать в виде:
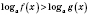
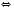
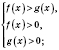
или
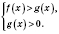
2. Если
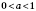
, то неравенство
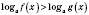
равносильно двойному неравенству
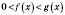
.
Это утверждение можно записать в виде:
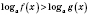
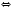
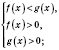
или
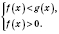
Обратите внимание: при решении логарифмической неравенства нет смысла отдельно выписывать ОДЗ, поскольку все равно будет необходимо решать систему неравенств, которая включает и ОДЗ.
Примеры
1)
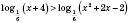
.
Логарифмическая функция
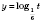
с основанием
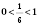
нисходящая, следовательно, данное неравенство равносильно системе
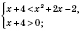
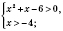
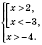
 Ответ
Ответ:
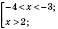
(или в виде
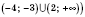
.
2)
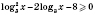
.
Пусть
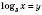
.
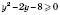
,
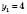
,
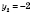
.
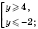
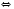
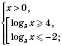
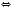
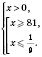
 Ответ
Ответ:
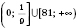
или
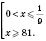
3)
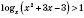
.
Рассмотрим два случая.
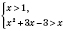
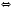
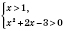
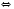
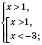
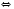
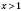
.
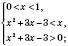
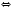
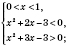
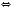
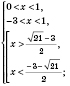
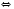
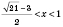
.
Объединяя эти промежутки, получим ответ.
Ответ:
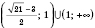
.
4)
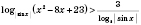
.
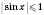
; основанием логарифма может быть только положительное число, которое не равно 1. Исходя из этого, получаем, что данное неравенство равносильно системе:
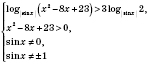
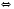
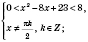
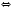
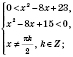
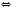
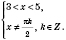
Если
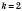
, то
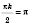
;
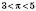
.
Если
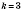
, то
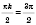
;
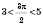
.
Ответ:
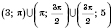
.