Урок № 12
Тема. Умножение дробей. Подъем дроби в степень
Цель: добиться усвоения учащимися содержания и схемы доведения правила умножения рациональных дробей, а также содержания алгоритма (ориентировочной схемы действий) умножение рациональных дробей; формировать умение воспроизводить изученные правила и алгоритм и применять их во время выполнения задач на умножение рациональных дробей; совершенствовать умения выполнять сокращение рациональных дробей и находить ОДЗ дробного выражения.
Тин урока: усвоение знаний, формирование первичных умений.
Наглядность и оборудование: опорный конспект «Умножение и деление рациональных дробей».
Ход урока
I. Организационный этан
На этом этапе урока следует предоставить учащимся информацию:
· ориентировочный план изучения раздела;
· количество учебных часов;
· примерное содержание материала;
· основные требования к знаниям и умениям учащихся;
· ориентировочное содержание заданий, которые будут вынесены на контроль.
(Эту информацию можно поместить на стенде «Справочно-информационный уголок» в кабинете математики и ради экономии времени предложить учащимся для самостоятельного ознакомления в неурочное время).
II. Проверка домашнего задания
Письменная часть домашнего задания (анализ контрольной работы) проверяется учителем после того, как он соберет тетради учащихся для проверки.
Качество выполнения учащимися устной части домашнего задания проверяется во время выполнения устных упражнений. Эту работу можно провести в форме математического диктанта на повторение.
III. Формулировка цели и задач урока, мотивация учебной деятельности учащихся
IV. Актуализация опорных знаний и умений
@ Для успешного восприятия учащимися учебного материала урока перед изучением нового материала следует активизировать знания и умения учащихся по правила умножения и сокращения дробей, основного свойства степени и ее последствий, разложение многочленов на множители, сокращение рациональных дробей и правила знаков для рациональных дробей.
Выполнение устных упражнений
1. Вычислите: 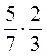 ;
; 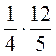 ;
; 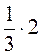 ;
; 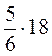 ;
; 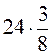 ;
; 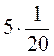 .
.
2. Представьте в виде степени с основанием у выражения: в ∙ у3; у10 ∙ у2; 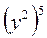 ;
; 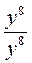 ; у18 ∙ у2;
; у18 ∙ у2; 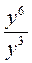 ;
; 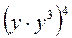 .
.
3. Разложите выражение на множители:
а) ах - а; б) х2 + 1 - 2х; в) х2 + 8х; г) 2у2 - 8; д) у3 - x2y; е) k3 - x3; ж) 4х2 + 16х + 16; с) 27 + 3у2 - 18у.
4. Каких значений (равных или противоположных) приобретают при одном и том же значении переменной выражения:
а) - х и х; б) х - 2 и 2 - х; в) 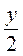 и
и 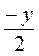 ; г)
; г) 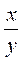 и
и 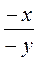 ; д)
; д)  и
и 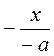 ; е)
; е) 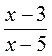 и
и 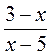 ?
?
V. Усвоение знаний
План изучения нового материала
1. Правило умножения рациональных дробей (с доводкой).
2. Алгоритм умножения рациональных дробей; примеры его применения.
@ Традиционно изучение вопроса о преобразовании произведения рациональных дробей на рациональный дробь начинается с формулировки правила умножения рациональных дробей в словесной форме и в виде формулы
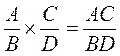
(которая выполняется при всех допустимых значениях переменных). Справедливость этой формулы доказывается путем рассуждений, основанных на представлении о дробь как особую форму записи доли двух выражений и на свойствах компонентов действия деления (как в доказательстве правил сложения и вычитания рациональных дробей и основного свойства дроби).
Так же как во время изучения сложения и вычитания рациональных дробей после доведения справедливости правила умножения рациональных дробей, на основе этого правила состоит схема (алгоритм) выполнения действий, которые должны привести от произведения рациональных дробей к рациональной дроби.
Применение составленного алгоритма следует продемонстрировать на разноплановых примерах.
Для большей наглядности на уроке служит опорный конспект «Действия над рациональными дробями».
Конспект 4 |
Умножение и деление рациональных дробей |
|
1. Для любых А, В, С и D где В ≠ 0, D ≠ 0, выполняется равенство: 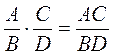 |
|
|
|
2. Для любых А и В, В ≠ 0, выполняется равенство: 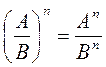 |
|
|
|
3. Для любых А, В, С и D где B ≠ 0, C ≠ 0, D ≠ 0, выполняется равенство: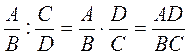 |
|
Замечания. Дробь, которым записывается произведение или часть дробей необходимо (если это возможно) сократить! Записывать его рациональным дробью - только исходя из условия задачи |
VI. Формирование умений
Выполнение устных упражнений
1. Прокомментируйте (согласно алгоритму выполнения действий в выражениях:
а) 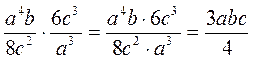 ;
;
б) 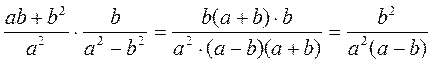 .
.
2. Представьте в виде дроби выражение:
а) 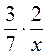 ; б)
; б) 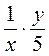 ; в)
; в) 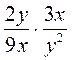 ; г)
; г) 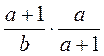 ; д)
; д) 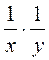 ; е)
; е) 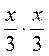 .
.
3. При а = 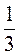 найдите значения выражений:
найдите значения выражений: 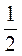 а;
а; 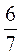 а;
а; 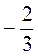 а;
а; 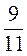 а.
а.
Выполнение письменных упражнений
Для реализации дидактической цели урока следует решить задачи следующего содержания:
1. Умножение рациональных дробей (в разных ситуациях: на прямое применение правила умножения рациональных дробей, с возможностью сокращения рационального дроби, с необходимостью разложения многочленов в числителе и знаменателе дроби на множители, для случае как двух, так и большего количества множителей).
1) Выполните умножение: а) 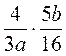 ; б)
; б) 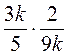 ; в)
; в) 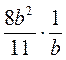 ; г)
; г) 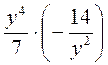 ; д)
; д) 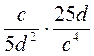 ; е)
; е) 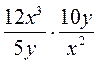 ; ж)
; ж) 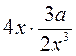 ; з)
; з) 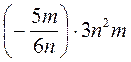 .
.
2) Выполните умножение: а) 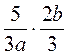 ; б)
; б) 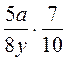 ; в)
; в) 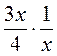 ; г)
; г) 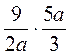 ; д)
; д) 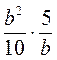 ; е)
; е) 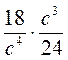 ; ж)
; ж) 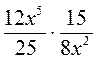 ; з)
; з) 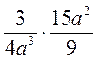 .
.
3) Упростите выражение: а) 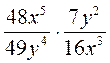 ; б)
; б) 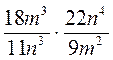 ; в)
; в) 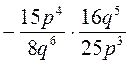 ; г)
; г) 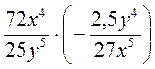 ; д)
; д) 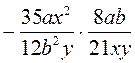 ; е)
; е) 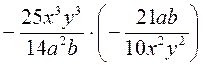 .
.
4) Выполните умножение: а) 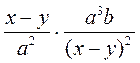 ; б)
; б) 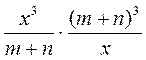 ; в)
; в) 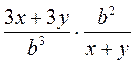 ; г)
; г) 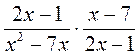 ; д)
; д) 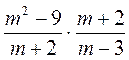 ; е)
; е) 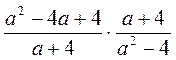 .
.
5) Упростите выражение:
а) 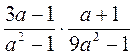 ; б)
; б) 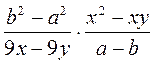 ; в)
; в) 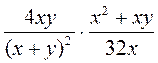 ; г)
; г) 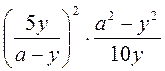 ; д)
; д) 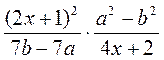 ; е)
; е) 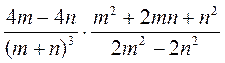 ; ж)
; ж) 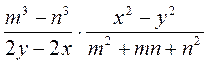 ; з)
; з) 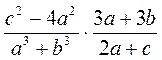 .
.
6) Выполните умножение:
а) 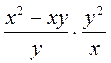 ; б)
; б) 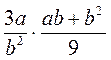 ; в)
; в) 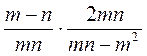 ; г)
; г) 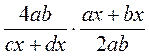 ; д)
; д) 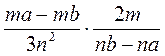 ; е)
; е) 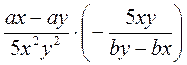 .
.
2. Выполнение упражнений на повторение: сложение (вычитание рациональных дробей с одинаковыми и разными знаменателями.
1) Представьте выражение в виде дроби:
а) 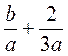 ; б)
; б) 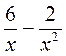 ; в)
; в) 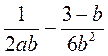 ; г)
; г) 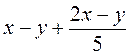 ; д)
; д) 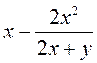 ; е)
; е) 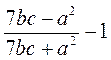 .
.
2) Упростите выражение:
а) 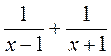 ; б)
; б) 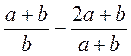 ; в)
; в) 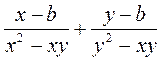 .
.
3) Упростите выражение:
а) 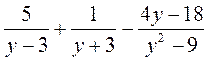 ; б)
; б) 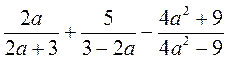 ; в)
; в) 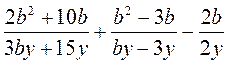 ; г)
; г) 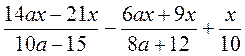 ;
;
д) 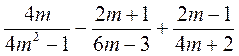 ; е)
; е) 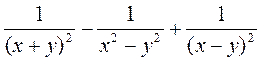 ; ж)
; ж) 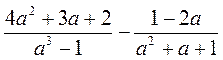 ; з)
; з) 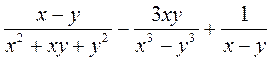 .
.
3. Выполнение логических упражнений и заданий повышенного уровня сложности для учащихся, имеющих достаточный и высокий уровни знаний.
1) Выполните умножение:
а) 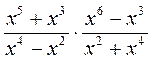 ; б)
; б) 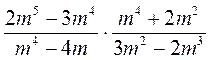 .
.
2) Упростите выражение:
а) 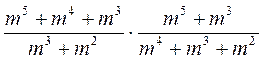 ; б)
; б) 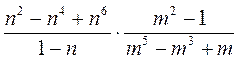 .
.
3) Выполните действия:
а) 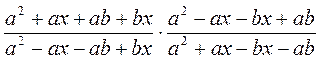 ; б)
; б) 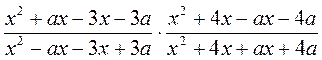 .
.
4) запись пропущено:
@ Упражнения, предлагаемые для решения на урок, должны быть направлены на усвоение навыков быстрого и безошибочного преобразования произведения двух рациональных дробей в рациональный дробь. Этого можно добиться за счет достаточно большого количества упражнений различного уровня сложности (см. выше).
Следует заметить, что в преобразовании произведения рациональных дробей широко используются: формулы сокращенного умножения, правило изменения знака дроби, различные приемы разложения многочленов на множители. Во время устной работы на уроках полезно предлагать учащимся упражнения на повторение этих моментов.
Обратим внимание также на то, что было бы ошибкой во время изучения умножения рациональных дробей выполнять упражнения только на умножение, отказавшись от выполнения действий сложения и вычитания рациональных дробей и от сравнения правил выполнения этих действий. Для формирования устойчивых навыков выполнения сложения и вычитания рациональных дробей (как известно, это требует достаточно большого промежутка времени) в ходе изучения как умножение, так и деление рациональных дробей через систему устных и повторювальних упражнений следует продолжать работу по совершенствованию умений учащихся выполнять сложение и вычитание рациональных дробей.
VII. Итоги урока
В любом из случаев правильно выполнено умножение рациональных дробей?
а) 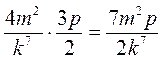 ; б)
; б) 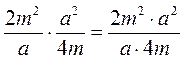 ; в)
; в) 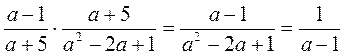 ?
?
VIII. Домашнее задание
1. Изучить правило умножения рациональных дробей (с доводкой).
2. Решить упражнения на усвоение алгоритма умножения рациональных дробей и отработки навыков его применения.
3. Решить упражнения на повторение алгоритмов сложения и вычитания рациональных дробей.
4. Повторить правило умножения обыкновенной дроби на целое число (справочник 6 класс), определение и свойства степени с натуральным Показателем и свойства умножения дробей (переставляющейся, соединительную и распределительную).
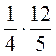 ;
; 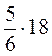 ;
; 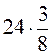 ;
; 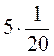 .
.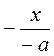 ; е)
; е) 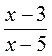 и
и 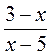 ?
?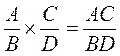
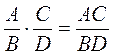
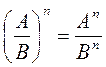
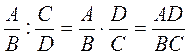
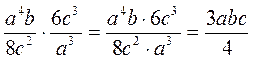 ;
;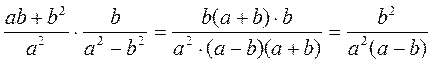
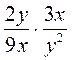 ; г)
; г) 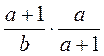 ; д)
; д) 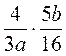 ; б)
; б) 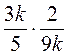 ; в)
; в) 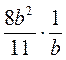 ; г)
; г) 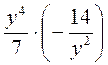 ; д)
; д) 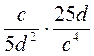 ; е)
; е) 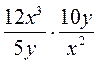 ; ж)
; ж) 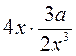 ; з)
; з) 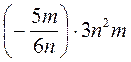 .
.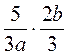 ; б)
; б) 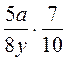 ; в)
; в) 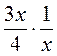 ; г)
; г) 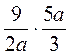 ; д)
; д) 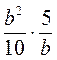 ; е)
; е) 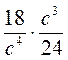 ; ж)
; ж) 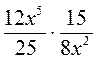 ; з)
; з) 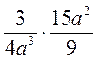 .
.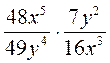 ; б)
; б) 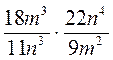 ; в)
; в) 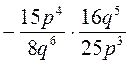 ; г)
; г) 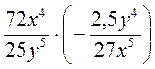 ; д)
; д) 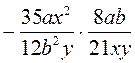 ; е)
; е) 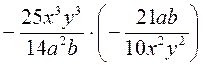 .
.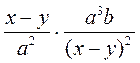 ; б)
; б) 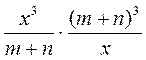 ; в)
; в) 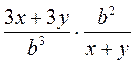 ; г)
; г) 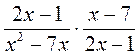 ; д)
; д) 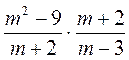 ; е)
; е) 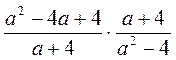 .
.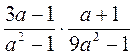 ; б)
; б) 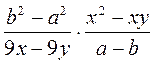 ; в)
; в) 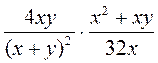 ; г)
; г) 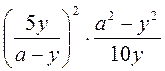 ; д)
; д) 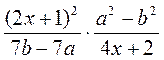 ; е)
; е) 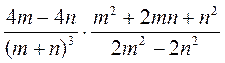 ; ж)
; ж) 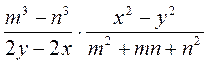 ; з)
; з) 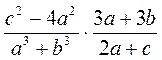 .
.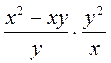 ; б)
; б) 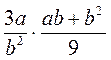 ; в)
; в) 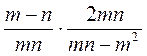 ; г)
; г) 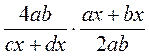 ; д)
; д) 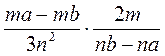 ; е)
; е) 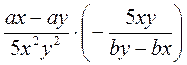 .
.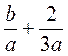 ; б)
; б) 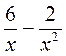 ; в)
; в) 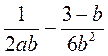 ; г)
; г) 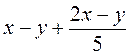 ; д)
; д) 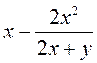 ; е)
; е) 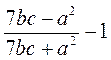 .
.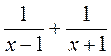 ; б)
; б) 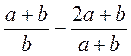 ; в)
; в) 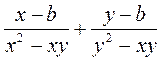 .
.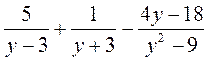 ; б)
; б) 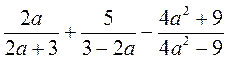 ; в)
; в) 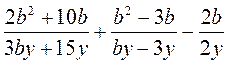 ; г)
; г) 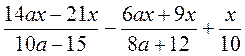 ;
;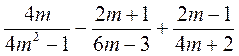 ; е)
; е) 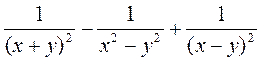 ; ж)
; ж) 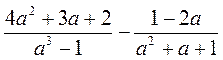 ; з)
; з) 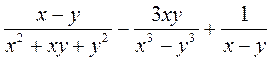 .
.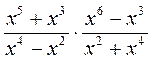 ; б)
; б) 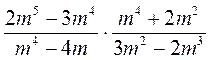 .
.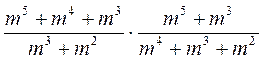 ; б)
; б) 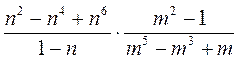 .
.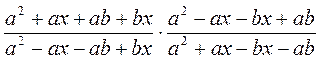 ; б)
; б) 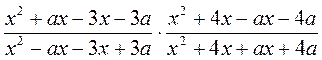 .
.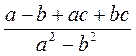
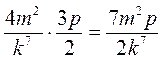 ; б)
; б) 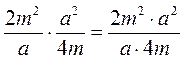 ; в)
; в) 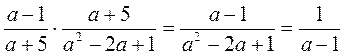 ?
?