УРОК № 12
Тема. Линейные неравенства с одной переменной
Цель урока: добиться закрепления учениками содержания: определение равносильных неравенств и свойств равносильных неравенств; определение линейного неравенства с одной переменной и схемы Те решения в зависимости от различных значений коэффициентов. Дополнить знания учащихся представлениям о схеме действий при решении неравенств с одной переменной, содержащих дроби с числовыми знаменателями. Продолжить работу по выработке умений: воспроизводить содержание изученных понятий и алгоритмов; применять их для решения упражнений, предполагающих решение линейных неравенств с одной переменной.
Тип урока: закрепление знаний, отработка умений.
Наглядность и оборудование: опорный конспект № 9, раздаточный материал (карточки с решениями упражнений домашнего задания).
Ход урока
I. Организационный этап
Учитель проверяет готовность учащихся к уроку, настраивает их на работу.
II. Проверка домашнего задания
Поскольку упражнения домашнего задания являются упражнениями репродуктивного (в основном) характера, то их проверку можно осуществить частично (только у учащихся, требующих дополнительного педагогического внимания) или предложить учащимся проверить ответы по образцу (правильные ответы заранее записаны за доской или розданы карточки с решениями для самостоятельной проработки).
III. Формулировка цели и задач урока.
Мотивация учебной деятельности учащихся
Для осознания учащимися необходимости изучения материала этого урока можно определенным образом создать проблемную ситуацию: предложив сначала задачи на повторение (решение уравнения с одной переменной соответствующего вида - см. домашнее задание на повторение), затем перенести ситуацию в новые условия - предложить для решения неравенство, которое отличается от развязанного уравнения только знаком (вместо знака равенства поставить знак неравенства). Таким образом формулируется проблема: возможно ли решить предложенную неравенство, совершая те же шаги, что и при решении уравнения (с учетом существующих различий в свойствах равенств и неравенств)? Поиск ответа на этот вопрос и является основной целью урока.
IV. Актуализация опорных знаний и умений учащихся
Устные упражнения
1. Есть правильной неравенство:
1) -8 : 2 10 : (-3);
2) 3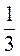 - 5 -1
- 5 -1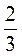 ;
;
3) 1 - 0,8 : 0,04 > -10;
4) 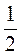 -
- 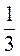 >
> 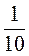 ;
;
5) 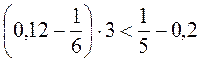 ?
?
2. Какие из чисел: 3; 3,14; 3,1403; n - являются решениями неравенства х 3,14?
3. Решите неравенство:
1) 1 - х 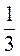 ;
;
2) -6х > 3;
3) 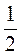 х + 2 > 0.
х + 2 > 0.
4. Запишите числовые промежутки, соответствующие рисунке:
V. Дополнение знаний
Методический комментарий
При работе над составлением схемы действий для решения неравенств с одной переменной, содержащие дробные коэффициенты, учащиеся должны осознать, что несмотря на существующее различие в свойствах числовых равенств и числовых неравенств схемы действий при решении уравнений и неравенств первой степени с одной переменной очень похожи. Дополнительно к вопросу о способ решения неравенств с одной переменной, содержащих дробные коэффициенты, желательно рассмотреть своего рода противоположный случай - когда для упрощения процесса решения неравенства целесообразно предварительно выполнить деления правой и левой частей неравенства на НСК коэффициентов правой и левой частей неравенства (для осознания способа соответствующих действий можно также предложить ученикам соответствующее уравнение с одной переменной). В любом случае после выполнения записи решения примеров учитель должен или сам, или привлекая к этому учеников сделать вывод о том, что как и при решении уравнений, так и при решении неравенств первое равносильное преобразование, которое желательно выполнить,- это умножение или деление обеих частей на одно и то же число с целью упрощения вида данной неровности.
Опорный конспект № 9
Основные шаги решения неравенств с одной переменной |
1. Если неравенство содержит дроби, то умножаем обе части неравенства на наименьший общий знаменатель всех дробей, входящих в неравенство. |
2. Если неровности есть скобки, то раскрываем их. |
3. Переносим слагаемые с переменной в одну часть неравенства, а остальные слагаемые - в вторую часть. |
4. Сводим подобные слагаемые, получаем линейное неравенство. Решаем линейное неравенство по схеме (см. опорный конспект № 8). |
Пример. Решим неравенство: |
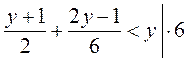 ; НСЗ (2; 6) = 6 ; НСЗ (2; 6) = 6
3(у + 1) + 2у - 1 6у;
3в + 3 + 2у - 1 6у; |
5y + 2 6y;
5в - 6в -2;
-в -2;
в > 2. |
Ответ: y  (2; +∞). (2; +∞). |
VI. Формирование умений
Устные упражнения
1. Решите неравенство:
1) 2x 8;
2) 3х ≥ 6;
3) 0х > 11;
4) 0х -7;
5) 0х 8;
6) 0x > -3;
7) 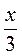 > 1;
> 1;
8) 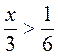 ;
;
9) 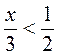 .
.
2. Упростите выражение:
1) 7(1 - 2x) + 5х;
2) 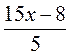 ∙ 5;
∙ 5;
3) 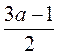 ∙ 4;
∙ 4;
4) х(х + 2) - 3х(х - 1).
Письменные упражнения
Для реализации дидактической цели урока следует решить упражнения такого содержания:
1) решить неравенства с одной переменной, содержащих дробные коэффициенты или целые коэффициенты, которые имеют общий делитель;
2) решить неравенства с одной переменной, требующих применения тождественных преобразований рациональных выражений;
3) на повторение: задачи на нахождение пересечения и объединения числовых промежутков, а также на повторение содержания понятия системы и совокупности неравенств с одной переменной.
Методический комментарий
Целью упражнений, предлагаемых для решения на уроке, является закрепление терминологии, изученной на предыдущем уроке, дальнейшее совершенствование навыков равносильных преобразований неравенств с одной переменной решение линейных неравенств с одной переменной, а также выработка "умений выполнять действия по схеме, составленной на предыдущем этапе урока.
VII. Итоги урока
Контрольное задание
Найдите и исправьте ошибки:
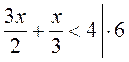 ;
;
6 ∙ 3x + 6 ∙ х 4;
24х 4;
x > 6.
Ответ: (6; + ∞).
VIII. Домашнее задание
1. Повторить содержание понятий, изученных на предыдущем уроке, а также изучить схему действий, составленную на данном уроке.
2. Решить упражнения, аналогичные по содержанию упражнениям классной работы.
3. На повторение: нахождение пересечения и объединения числовых промежутков.
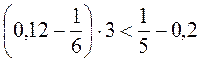
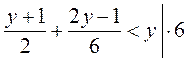 ;
; 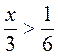
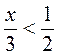 .
.