Показательные уравнения

Показниковими уравнениями называются такие уравнения, в которых неизвестное входит только в показатели степеней при постоянных основах.

Решение показательных уравнений

1. Решения сведением к общей основы
,
,
,
,
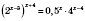
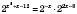
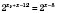
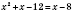
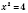
, x = ±2.
Ответ: x1 = 2; x2 = -2.
2. Показательные уравнения, имеющие показатели с одинаковой буквенной частью
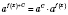
Очевидно, что , где C - const, .
1) .
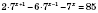
Вынесем за скобки общий множитель левой части :
,
,
,
,
.
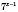
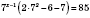
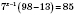
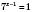
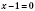
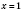
Ответ: 1.
2) .
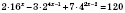
Сведем все степени к общей основы 2.
,
,
,
,
,
,
,
.
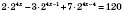
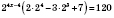
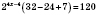
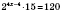
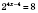
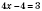
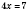
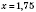
Ответ: 1,75.
3. Показательные уравнения, сводящиеся к квадратным
,
.
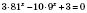
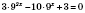
Пусть , .
;
. .
; ;
. .
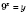
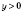
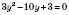
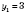
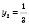
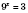
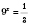
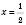
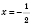
Ответ: ; .
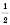
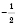
4. Однородные показательные уравнения
.
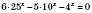
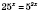
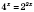
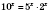
Обратите внимание, что , , . Следовательно, .
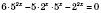
Все члены левой части этого уравнения имеют степень 2х, т.е. уравнение однородное. Поделим обе части его на :
.
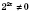
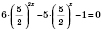
Пусть , .
;
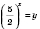
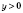
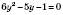
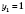
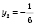
; не удовлетворяет условие .
; .
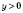
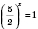
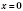
Ответ: 0.
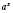
5. Уравнения, которые одновременно содержат и .
.
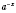
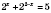
Умножим обе части уравнения на :
.
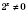
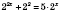
Пусть , .
;
. .
; ;
. .
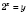
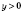
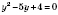
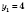
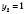
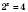
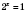
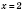
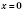
Ответ: 2; 0.
6. Показательные уравнения, содержащие обратные выражения
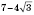
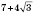
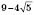
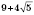
Обратите внимание: в уравнениях можно встретить выражения, произведение которых равно 1, например: и ; и и т. д.
.
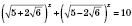
Пусть , .
,
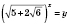
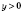
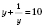
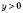
, следовательно, на y можно умножить обе части уравнения.
,
,
, .
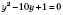
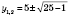
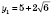
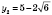
1) , .
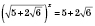
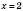
2) ,
,
; .
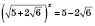
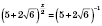
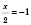
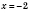
Ответ: 2; -2.
7. Для решения некоторых уравнений удобно использовать монотонность показательной функции
1) .
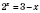
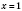
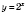
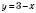
Очевидно, что является корнем уравнения. Функция является возрастающей, а функция - убывающая. Следовательно, уравнение не может иметь более чем один корень.
Ответ: 1.
2) ; .
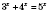
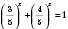
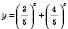
Функция является суммой двух возрастающих функций, то есть является возрастающей на R. Правая часть уравнения 1 - постоянная величина. Следовательно, уравнение не может иметь более чем один корень.
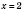
является корнем уравнения.
Ответ: 2.

Решения уравнений показниковостепеневих

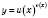
Показниково-степенная функция имеет вид . Ее область определения находим, рассматривая три случая:
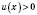
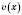
1) ; - любое число;
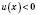
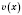
2) ; - целое число;
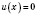
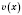
3) ; - целое положительное число.
Пример
Решить уравнение:
а) .
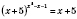
Рассмотрим случаи:
1) , .
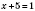
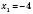
2) , .
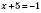
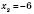
3) , .
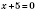
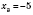
4) ; , .
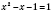
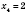
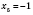
Проверкой убеждаемся, что все найденные корни уравнения удовлетворяют.
Ответ: -4; -6; -5; 2; -1.
б) .
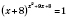
1) , .
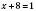
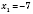
2) , .
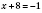
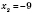
3) ; , .
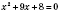
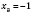
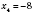
Проверка
1) , .
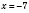
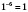
2) , .
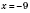
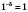
3) , .
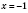
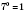
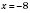
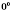
4) ; не имеет смысла.
Ответ: -7; -9; -1.

Решение показательных неравенств

В основе решения показательных неравенств лежит монотонность показательной функции, которая зависит от значения основы. Способы решения аналогичны способам решения показательных уравнений, но часто приводят к системе неравенств, потому что нужно учесть условие
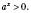Примеры
1) .
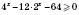
Пусть , .
; .
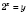
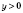
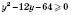
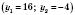
Получим систему неравенств:

; .
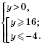
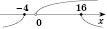
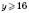
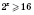
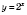
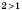
Показательная функция с основанием является возрастающей на R.
Следовательно, .
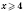
Ответ: .
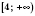
2) ;
.
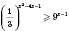
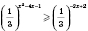
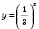
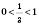
Показательная функция с основанием является убывающей на R, поэтому получим:
, ,
.
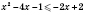
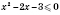
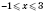
Ответ: .

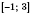
Назад

Содержание

Вперед