Обобщение понятия степени
Основные определения
1. Если
n Является
N,
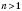
, то
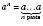
, где
a - произвольное число.
2.
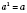
, где
а - произвольное число.
3.
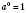
для
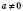
.
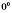
не имеет содержания.
4.
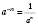
,
n Является
N,
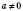
.
5.
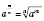
,
n Является
N,
m Є
Z,
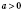
.
Свойства степени с рациональным показателем
Для любых рациональных чисел
r и
s и любых положительных
a и
b выполняются следующие равенства.
1.
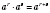
.
2.
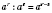
.
3.
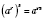
.
4.
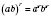
.
5.
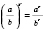
.
6. Если
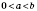
, то
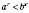
для
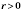
;
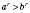
для
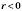
.
7. Если
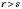
, то
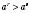
для
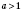
;
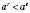
для
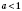
.
Понятие степени с иррациональным показателем
Пусть
a - любое положительное число, которое не равно 1,

- любое иррациональное число.
Рассмотрим три случая.
1.
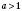
,
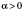
.
Например,
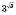
;
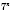
. Степень
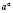
означает такое число, которое больше всякого степени
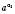
, но меньше от всякого степени
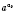
, где
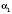
- любое рациональное приближение числа

, взятое с недостачей, а
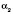
- любое приближение числа a, взятое с избытком. Обратите внимание: такое действительное число существует, и к тому же единственное.
2.
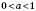
,
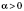
.
Например,
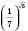
. Тогда под степенью
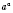
понимают число, которое меньше любого степени
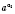
, но больше от любого степени
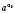
.
3.
a - произвольное число, кроме 1,
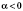
.
Например,
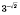
,
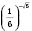
. Тогда считают
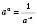
.
Действия над степенями с иррациональными показателями выполняются по тем же правилам, которые установлены для степеней с рациональными показателями.
Степенная функция
Функцию
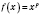
, где
x - переменная, а
p - фиксированное действительное число, называют
степенной функцией.
Свойства степенной функции зависят от значения
p.
1.
p Есть
N. Тогда
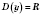
;
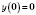
;
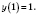
Если
p - нечетное, знак
y совпадает со знаком
x; функция нечетная и возрастает на всей области определения. Если
p - четное,
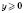
для всех значений
x; функция парная. Если
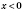
, то функция убывает, если
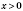
, то функция возрастает.
2.
p Є
Z;
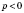
. Тогда
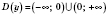
.
График состоит из двух ветвей;
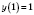
.
Если
p - нечетное, то для всех значений
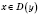
знак функции совпадает со знаком аргумента.
Функция нечетная, нисходящая на каждом из промежутков
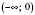
и
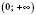
.
Если
p - четное,
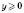
для всех
x; функция парная. Если
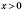
, то функция убывает, если
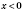
, то функция возрастает. На рисунках, представленных ниже, приведены графики степенной функции для разных значений
p:
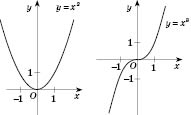
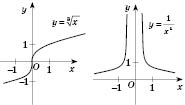
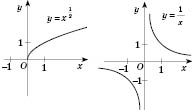
Показательная функция
Функция
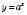
, где
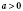
и
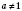
, называется
показниковою (с основой
а).
Свойства показательной функции
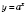
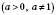
:
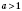
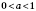
1.
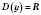
. 1.
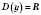
.
2.
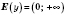
. 2.
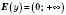
.
3. Функция не является ни четным, ни нечетным.
4. График функции расположен в верхней півплощині, пересекает ось
Оу в точке (0; 1), ось
Ох является для него асимптотою.
5. Функция возрастает 5. Функция спа на
R. дает на
R.
6. Если
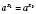
, то
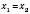
.
7. Если
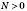
, то существует, и к тому же единственное, значение
x, при котором
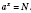
(Т.е. уравнение
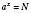
всегда имеет решение, и к тому же единственный, если
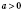
,
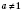
,
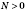
.)
На рисунке внизу слева изображен график показательной функции
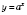
при
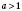
; на рисунке 1 - при
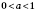
.
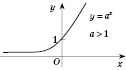
Рис. 1
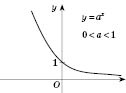
Рис. 2