Урок № 126

Тема. Решение задач геометрического содержания

1. На координатной прямой отметьте точку D(-3) и точку С, чтобы длина CD равнялась 2,5 единичных отрезка. Определите координату точки С. Сколько решений имеет задача?

2. Найдите площадь и периметр четырехугольника ABCD, если A(-1; 2); B(3; 2); С(3; -4); D(-1; -4).

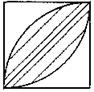
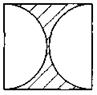
3. Найдите площади заштрихованных фигур, изображенных на рисунке ниже, если стороны квадратов равны по 10 см.

1)

2)

3)

4)

4. В какой части координатной плоскости расположены точки, координаты которых имеют: а) одинаковые знаки; б) противоположные знаки. Где находятся точки, в которых одна из координат равна 0?

5. Постройте ΔABC, если А(-5; -2); B(0; 4); С(3; -5). Назовите координаты каких-либо двух точек, одна из которых лежит внутри, а вторая - снаружи треугольника.

6. Постройте четырехугольник ABCD по координатам его вершин и найдите координату точки, в которой пересекаются его диагонали, если A(-2; -2); B(-3; 2); С(1; 4); D(2; -3).

7. Начертите на координатной плоскости треугольник LPQ, если L (-3; -4), P(0; 4), Q(5; -1). Найдите координаты точек пересечения стороны PQ с осью х и стороны LГ с осью у.

8. Постройте на координатной плоскости точки:

а) A(-4; -2); B(-3; -1); С(-2; 0); D(-1; 1);

б) M(2; 6); N(3; 4); P(4; 2); K(5; 0);

в) X(-2; -5); Y(-2; -2); Z(-2; 1).

Эти точки расположены в определенной последовательности. Установив ее, отметьте 2-3 точки. Назовите их координаты.

9. На листе бумаги отмечены 2 точки: А и В. Нарисуйте на этом листе такую систему координат, чтобы A(2; 3) и B(-2; 3).

10. Постройте график движения лодки, который движется против течения реки, в течение 6 часов после отплытия от пристани, если собственная скорость 6 км/ч, а скорость течения 3,5 км/ч.