УРОК № 11
Тема. Линейные неравенства с одной переменной
Цель урока: добиться усвоения учащимися содержания понятий: линейное неравенство с одной переменной, равносильные неравенства, равносильные преобразования неравенства и способов равносильных преобразований неравенств; схемы решения линейных неравенств с одной переменной. Выработать умения: воспроизводить содержание изученных понятий и алгоритмов; выполнять действия согласно схемы решения линейных неравенств с одной переменной и простейшие равносильные преобразования неравенств с использованием свойств числовых неравенств и следствий из них.
Тип урока: формирование знаний, выработка первичных умений.
Наглядность и оборудование: опорный конспект № 8.
Ход урока
I. Организационный этап
Учитель проверяет готовность учащихся к уроку, настраивает их на работу.
II. Проверка домашнего задания
Поскольку упражнения домашнего задания являются упражнениями репродуктивного (в основном) характера, то проверку домашнего задания можно осуществить или частично (только у учащихся, требующих дополнительного педагогического внимания), или можно предложить учащимся проверить ответы (правильные ответы заранее записаны за доской или розданы как карточки для самостоятельной проработки), или провести диагностическую самостоятельную работу [8, самостоятельная работа № 3, задача 1] с последующей проверкой.
III. Формулировка цели и задач урока.
Мотивация учебной деятельности учащихся
Для осознания учащимися необходимости изучения нового материала можно определенным образом создать проблемную ситуацию: предложить учащимся выполнить задания на проверку того, является ли данное число решением неравенства с одной переменной, а затем решить ту же неравенство (напомнив предварительно, что решить неравенство означает найти все ее решения или доказать, что их нет). Осознание учащимися невозможности решения конкретной задачи с применением тех знаний и умений, которыми они владеют, создает мотивацию к изучению вопроса о видах и способах решения простейших неравенств с одной переменной. Таким образом формулируется дидактическая цель урока, а также выделяются задания для учеников на урок.
IV. Актуализация опорных знаний и умений учащихся
Устные упражнения
1. Какое из чисел: -2; 3 - являются решением неравенства:
1) (х - 1)(х + 2) > 0;
2) 2х - 3 0?
2. Принадлежит промежутку [-3; 5,2) число:
1) -3; 2) 0; 3) 5; 4) 5,2; 5) 6?
3. Известно, что 5 а 7. Оцените значение выражения:
1) а + 1; 2) 3; 3) а - 3; 4) -3а; б) 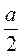 - 1; 6)
- 1; 6) 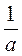 .
.
4. Упростите выражение:
1) 4(x - 3) + 1;
2) 12 - 3(1 - 2x);
3) 5(2z + 7) + 14(5 - z);
4) х2 - 3х - 8 - х(х + 2).
5. Решите уравнение:
1) 3х = 6; 2) 0х = 0; 3) 0х = -3.
V. Формирование знаний
План изучения нового материала
1. Понятие равносильных неравенств. Равносильные преобразования неравенств.
2. Понятие линейного неравенства с одной переменной.
3. Схема решения линейного неравенства с одной переменной.
4. Как решить неравенство с одной переменной, что сводится к линейной. Примеры.
Методический комментарий
Согласно данного плана изложения материала формирование знаний учащихся на данном уроке начинается с изучения определения равносильных неравенств с одной переменной и продолжается изучением формулировок основных теорем равносильности (которые даются без доказательства и объясняются на примерах). Для лучшего понимания учащимися этого фрагмента материала урока можно предложить им сравнить свойства числовых равенств и неравенств и таким образом выявить как схожие, так и отличительные их черты. Результатом такого сравнения будет осознание учащимися существование определенных аналогий между понятиями «уравнение и его решения» и «неравенство и ее решения» и средств решения как одних, так и других (и акцентировать внимание на различиях - при умножении или делении обеих частей неравенства на отрицательное число). Обратим внимание, что в разных источниках определение линейного неравенства с одной переменной даются несколько по-разному: в традиционных учебниках последних лет это неравенство вида ax > b (ax b, ax ≥ b, ax ≤ b), а например, в таблицах по алгебре для 7-11 классов [7] это неравенство вида ax + b > 0 (ax + b 0, ax + b ≥ 0, ax + b ≤ 0). Учащимся можно продемонстрировать оба определения и показать, что отличие первого состоит только в том, что описываемую неравенство уже сведено к виду, аналогичному виду линейных уравнений с одной переменной (ах = b).
Сравнивая линейные неравенства с одной переменной и линейные уравнения с одной переменной, следует заметить, что, учитывая существующую отличие рівносильної свойства (см. умножения или деления обеих частей неравенства на отрицательное число), в зависимости от знака неравенства, можно составить не одну схему решения линейного неравенства с одной переменной (особенно это касается случая, когда число равно 0), поэтому акцент надо делать не на заучивании схем, а на понимании действий, которые скрыты за этими схемами).
Завершающий этап изучения нового материала является практической частью (которая может быть подана как ответ на вопрос, поставленный в начале урока): на примере неравенства с одной переменной во время комментирования составляется примерная схема действий при решении неравенства с одной переменной, что сводится к линейной. Во время комментирования также уместным будет проведение параллелей с решением соответствующего уравнения с одной переменной.
Опорный конспект № 8
Два неравенства называют равносильными, если они имеют те же развязки. |
Некоторые равносильные преобразования неравенств |
1. Если из одной части неравенства перенести в другую часть слагаемые с противоположными знаками, то получится неравенство, равносильно данному. Например: 2x - 3 > 6 и 2х > 9-равносильны неравенства. |
2. Если обе части неравенства умножить (или разделить) на одно и то же положительное число, то получится неравенство, равносильно данному.
Например: 2x > 6 и х > 3, 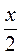 > 6 и x > 12-равносильны неравенства. > 6 и x > 12-равносильны неравенства. |
3. Если обе части неравенства умножить (разделить) на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится неравенство, равносильно данному. |
Например: -3х > 6 и x -2; 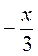 > 6 и x - 18-равносильны неравенства. > 6 и x - 18-равносильны неравенства. |
Линейное неравенство с одной переменной - неравенство вида ах > bили ах b, или ах ≥ bили ах ≤ b, где а, b - данные числа, ах - переменная.
Например: 3х > 1; -x -3; 0х > 3; 0х 0-линейные неравенства. |
Схема решения линейного неравенства |
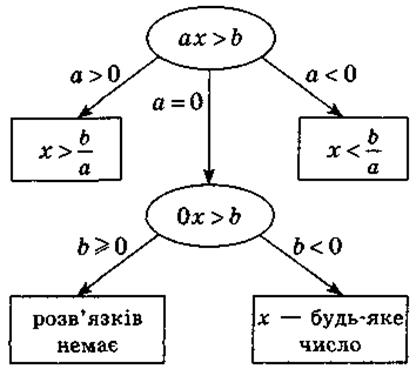
|
Пример решения неравенства, сводится к линейной: |
Решить неравенство
9(х - 1) + 5х 17х - 11 |
Комментарий |
9х - 9 + 5х 17х - 11
14х - 9 17х - 11 |
1. Выполним тождественные преобразования левой (и правой) частей неравенства. |
14х - 17х -11 + 9
-3х -2 |
2. Перенесем известные слагаемые в одну часть неравенства, а неизвестные - в другую.
Тождественно преобразуем обе части. |
х > 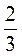 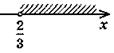
x  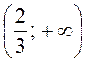
Ответ: 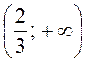 |
3. Поскольку коэффициент при х в левой части образованной неровности не равна нулю, разделим на него обе части неравенства, изменив его знак на противоположный (бу -3 0). Запишем соответствующий числовой промежуток - это и есть ответ - решение данного неравенства. |
VI. Формирование умений
Устные упражнения
1. Определите и обоснуйте, равносильны данные неровности.
1) 3х > 3 и х > 3;
2. 2) 3х > 3 и х > 1;
3) 3 + х > 5 и х > 5;
4) 3 + х > 5 и х > 2.
3. Решите неравенство:
1) 3х > 3;
2) х + 3 > 5;
3) -3х > 3;
4) х - 3 > 5;
5) -х 6;
6) 0х 7;
7) 0х > 7.
4. Упростите выражение:
1) 8х - (х + 2);
2) 8х - 5(х + 2);
3) 9(х - 3) - 5(х + 2).
Письменные упражнения
Для реализации дидактической цели урока следует решить упражнения такого содержания:
1) проверить, являются ли данные два неравенства равносильны (используя свойства равносильности неравенств);
2) решить неравенства с одним неизвестным, сводящихся к линейным неравенством с одной переменной путем применения одного из изученных равносильных преобразований;
3) решить неравенства с одним неизвестным, сводящихся к линейным неравенством с одной переменной путем применения нескольких (или всех) изученных равносильных преобразований;
4) на повторение: уравнения с одним неизвестным, сводящиеся к линейным уравнениям с одной переменной путем предварительного умножения (или деления) обеих частей уравнения на одно и то же число - наименьший общий знаменатель всех дробей (или наибольший общий делитель всех коэффициентов).
Методический комментарий
Решение упражнений на этом этапе урока следует начать с упражнений, способствующих закреплению учащимися содержания понятий «равносильные неравенства» и «равносильные преобразования неравенств». При этом в процессе решения таких упражнений следует требовать от учащихся сознательного комментирования своих действий с использованием изученной терминологии.
Следующая группа задач имеет целью способствовать закреплению у учащихся знаний относительно схемы решения линейных неравенств с одной переменной и выработке у учащихся устойчивых умений решать линейные неравенства с одной переменной, так и выполнять равносильные преобразования неравенств с одной переменной.
Только убедившись в том, что основные навыки решения простейших неравенств с одной переменной у учащихся произведено, можно переходить к более сложным примерам, которые способствуют совершенствованию навыков тождественных преобразований.
Чтобы подготовить учеников к восприятию материала следующего урока (решение неравенств, содержащих дроби с числовыми знаменателями), на данном уроке учащимся предлагается несколько примеров на повторение: решение уравнений соответствующего вида.
VII. Итоги урока
Контрольные вопросы
1. Два неравенства называют равносильными?
2. Как (какими способами) можно с данной неравенства (с одной переменной) образовать равносильное ему неравенство?
3. Неравенства вида которого называют линейными неровностями с одной переменной? Приведите примеры.
4. Какие решения может иметь неравенство ах > b, если:
1) а > 0;
2) а 0;
3) а = 0, b > 0;
4) а = 0, b 0?
VIII. Домашнее задание
1. Изучить содержание утверждений, рассмотренных на уроке (см. опорный конспект № 8).
2. Решить упражнения на закрепление содержания понятия «равносильные преобразования неравенств» и на выработку умений решать линейные неравенства с одной переменной и такие, которые сводятся к линейным путем простейших равносильных преобразований (аналогичные по содержанию и уровню сложности упражнениям классной работы).
3. На повторение: решить уравнение (аналогичные решенным в упражнениях на повторение - см. классную работу) и решить упражнения на нахождение ОДЗ рациональных выражений.