Графики тригонометрических функций

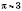
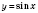
Для построения графиков тригонометрических функций возьмем . Построим график функции (см. рисунок).

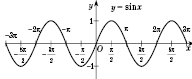
Эта кривая называется синусоидой.
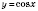
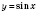
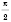
График функции можно получить из графика функции параллельным переносом его влево вдоль оси Ox на единиц. Это следует из формулы .

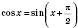
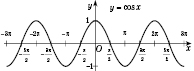
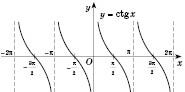
Построим график функции :

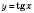
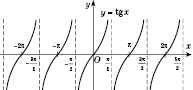
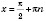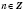
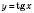
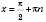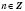
Обратите внимание: значение , не входят в область определения функции . Прямые , являются асимптотами графика. График носит название тангенсоїди.
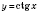
График функции легко получить, воспользовавшись формулой возведения :

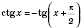
Рассмотрим график функции
.
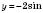
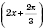
Запишем функцию в виде
.
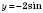
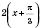
Из этого следует, что график этой функции можем получить, если построить:
1) график функции ;
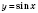
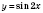
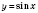
2) график функции , сжимая график функции в два раза к оси Oy;
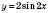
3) график функции , растягивая в два раза вдоль оси Oy график функции ;
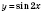
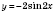
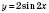
4) график функции , отображая график функции симметрично относительно оси Ox;
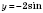
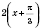
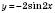
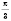
5) график функции , параллельно перенося график на расстояние влево вдоль оси Ox.
На рисунке не показаны постепенные преобразования графика, а только окончательный вид графика функции :

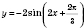
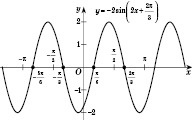
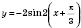
Обратите внимание: на практике можно сразу построить график функции , если учесть следующие соображения:
1) график будет иметь вид синусоиды;
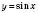
2) точка графика с координатами (0; 0) перейдет в искомом графике в точку ;
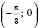
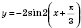
3) период функции равен ;
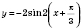
4) максимальные и минимальные значения функции соответственно равны 2 и -2;
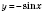
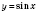
5) синусоида симметричная синусоиде относительно оси Ох.
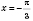
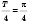
Таким образом, при росте значений аргумента от до бесконечности с шагом функция примет значение 0; -2; 0; -2; 0... и т. д.
Аналогично можно рассуждать, если надо построить графики функций:
y = Acos(kx+b);
y = Atg(kx+b);
y = Actg(kx+b).
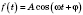
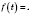
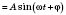
Величины, которые изменяются по закону или , называются гармоническими колебаниями.
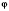
При этом: A - амплитуда колебаний; - круговая частота колебания; - начальная фаза колебания.
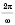
Период функции - период гармонического колебания.