Периодичность тригонометрических функций
Функция
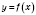
называется
периодической с периодом
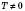
, если для любого
x из области определения функции числа
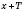
и
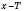
также принадлежат области определения и выполняется условие:
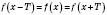
.
Если
T - период функции
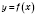
, то все числа вида
nT, где
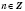
,
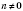
, также являются периодами функции.
Чтобы построить график периодической функции с периодом
T, достаточно построить график на отрезке длиной
T, а затем сделать параллельный перенос полученного графика на расстоянии
nT вправо и влево вдоль оси
Ox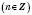
.
Тригонометрические функции являются периодическими. Наименьшим положительным периодом функции
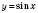
и
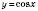
является
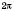
. Наименьшим положительным периодом функции
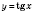
и
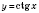
есть число

.
Итак:
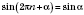
;
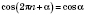
;
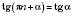
;
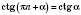
.
Теорема. Если функция
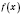
является периодической и имеет период
T, то функция
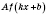
, где
A,
k,
b - некоторые числа, а
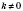
, тоже является периодической, период ее равен
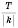
.
Так, периодом функции
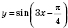
является число
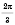
, периодом функции
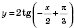
является число
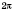
.
Свойства тригонометрических функций и их графиков