Урок № 112

Тема. Координатная плоскость

Цель: закрепить знание содержания основных понятий темы; выработать умение строить точки с заданными координатами и решать задачи, предусматривающие применение этих умений.

Тип урока: применение знаний, умений, навыков.

Ход урока

I. Организационный момент

II. Проверка домашнего задания

1. Проверяем так: на доске записать только координаты точек (можно добавить «лишние», которые предусматривают возможные ошибки учеников), а ученики должны написать рядом с координатой отметку точки (например, на доске записаны ...(-1; 2), а ученик вписывает B и т. д.)

№ 2 и № 3 являются задачами на повторение, поэтому проверяем решение так: ответ и называем свойство, использованную во время решения.

2. Для фронтальной проверки усвоения теоретических фактов, предлагаем ученикам выполнить

Математический диктант

Вариант 1[2]

1. Сколько чисел надо указать, чтобы задать положение точки на координатной плоскости? [Как называются числа, задающие положение точки на координатной прямой?]

2. Как называется первое [второе] из чисел, задающих положение точки на координатной плоскости?

3. Запишите обозначение точки Р [С], если ее абсцисса равна 0, а ордината 5 [абсцисса 5, а ордината 0].

4. Чему равна ордината [абсцисса] точки A(-1;-4) [M(-2;-3)]?

5. В левой или правой [верхний или нижний] части координатной плоскости находится точка X(6; -3) [А(7; -4)]?

III. Воспроизведение знаний

Во время проверки результатов выполнения математического диктанта учащиеся демонстрируют свои знания, которые получили на предыдущем уроке и во время изучения теории дома.

IV. Мотивация учебной деятельности

Учитель. Вы уже знаете, как определить координаты точки на координатной плоскости (см. рис). Теперь поставим обратную задачу: как по данным координатам определить положение точки на координатной плоскости.

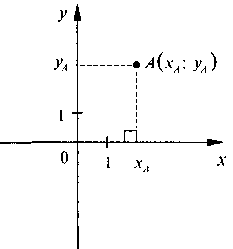
Определение координат точки

1. С т. А перпендикуляр до пересечения с Ох; имеем: хА - абсцисса т. А.

2. С т. А перпендикуляр до пересечения с Оу; имеем: са - ордината т. А. Точка А имеет координаты) (хА; уА).

V. Дополнение знаний

Задача. Пусть надо найти положение т. А(4;3) (построить т. А(4;3)).

Для этого:

а) найдем на оси Ох точку, что имеет координату 4, и проведем через нее прямую, которая перпендикулярна Ох;

б) найдем на оси Оу точку, что имеет координату 3, и проведем через нее прямую, перпендикулярную оси Оу.

Точка пересечения построенных перпендикулярных к осям прямых - искомая т. А.

Заметим, что, пользуясь разметкой (клеточки в тетради, миллиметровая бумага), прямые, перпендикулярные к осям, можно проводить «в уме», в воображении.

VI. Закрепления знаний. Совершенствование умений

@ Всю оставшуюся часть урока, то осталась, посвящаем выработке умений:

а) строить точки с заданными координатами (используя изученные свойства координат точек в координатной плоскости);

б) продолжаем работу по выработке умений определять координаты точки с готовыми рисунками;

в) решению поисковых задач (учимся наблюдать и делать выводы).

Письменные упражнения

1. Постройте систему координат, взяв единичный отрезок длиной 1см, и отметьте точки А(2; 1), В(-1;-3), С(0; -2), D(5; 0), M(-5; 1), N(3; -5).

@ Желательно задание выполнять так: сначала по координатам установить место нахождения точки (координатная четверть или координатная ось), а потом уже строить точки.

2. Постройте точку A(-3; 5) и точку В, координатами которой являются числа, противоположные соответствующим координатам точки А. Проведите отрезок АВ. Как располагается начало координат относительно отрезка АВ?

3. На координатной плоскости постройте несколько точек, каждая из которых имеет равные абсцису и ординату. Лежат ли эти точки на одной прямой?

4. На координатной плоскости начертите четырехугольник KLMN, если К(2; -3), L(2; 4), M(-2; 4), N(-2; -3). Каким является этот четырехугольник? Определите длину его сторон (в единичных отрезках) и вычислите его периметр.

5. Постройте на координатной плоскости точки A(5; 0), B(4; 3), C(3.4), D(0; 5), E(-3; 4), K(-4; 3), L(-5; 0), M(-4, -3), N(-3; -4), Q(0; -5), Р(3; -4), S(4; -3) и окружность с центром в т. А с радиусом 5 единичных отрезков. Убедитесь, что построенные точки лежат на этом круге.

Дополнительные упражнения

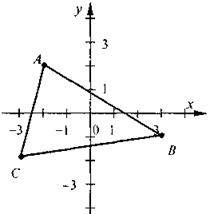
1. Какие координаты имеют вершины треугольника ABC (см. рис)? По рисунку найдите точки пересечения стороны АС с осью Ох; стороны ВС с осью Оу.

2. На 5 кг муки получили 2,25 кг припіку хлеба. Сколько процентов составляет прижегов от массы муки? от массы хлеба?

VII. Итоги урока

Как построить точку с известными координатами?

На каком из рисунков правильно изображено точку М(-1; 2)?

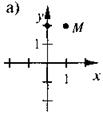
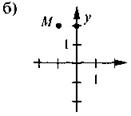
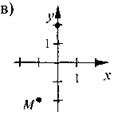
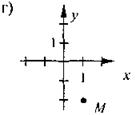
VIII. Домашнее задание

1. Постройте систему координат, взяв единичный отрезок 2 см, и отметьте точки: А(4; -1), В(-4; -1), С(5; -3), D(5; 2), М(-2; 0), N(0; 4).

2. Постройте точку С(-4; -1) и точку D, координаты которой равны модулям соответствующих координат точки С.

3. На координатной плоскости нарисуйте треугольник KLM, если К(-3;-1); L(1; -1); M(0; 3).

4. В совхозе с 5 000 га земли картофелем засажено 30 % площади, 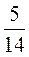остальных засеяно кормовыми культурами, а остальные - зерновыми культурами. Определите площадь под зерновыми.