Урок 112
Тема. Среднее
арифметическое. Средние величины
Цель: закрепить знания
учащимися содержания понятия среднее арифметическое чисел; сформировать понятие
средней величины (скорости, цены) и умение решать задачи на
нахождение значений первоначальных величин.
Тип урока:
применение знаний, навыков и умений.
Ход урока
I. Разминка
Устные упражнения
1.
Найдите
среднее арифметическое чисел:
1) 9,1 и 9,3; 2)
2,2; 2,3 и 2,4; 3) 0,3; 0,5; 0,7 и 1,5.
2. Может ли среднее арифметическое двух
последовательных натуральных чисел быть натуральным числом?
3. Решите уравнение:
1) 2,7 + а = 5,6;
2) b - 0,4 = 4,6;
3) с 1,64 + 1,36 с =
4,8;
4) 8d - 0,8d = 720.
4. Автомобиль ехал 4
ч со скоростью 54 км/ч и 2 часа со скоростью 60 км/ч. Какое расстояние он
преодолел на 6 ч.?
II. Проверка
домашнего задания
Учитель заранее
кратко записывает решение упражнений домашней работы, и ученики сверяют свои
ответы с записанными, при необходимости делают пояснения.
III. Совершенствование
знаний
Беседа
На предыдущем
уроке мы с вами рассмотрели примеры так называемых «средних значений» (средняя
температура месяца, среднее количество осадков за месяц, средняя заработная плата
т.п.).
Также мы рассмотрели
особый случай средних величин среднее арифметическое нескольких чисел. Давайте
вспомним, как называется среднее арифметическое нескольких чисел.
Можно
применить понятие среднего арифметического для нахождения средних величин?
Рассмотрим пример 1 (учебник, п. 33)
Автомобиль ехал со
скоростью 60 км/ч. Найдите среднюю скорость автомобиля на протяжении всего
пути.
Решения.
Комментарий. Мы знаем, что вообще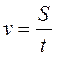 
, где v - скорость движения; S
- путь, t - время движения, поэтому для нахождения искомой скорости
найдем весь путь, потом общее время движения и поделим найденное значение
пути на общее время.
1) 54 · 4 + 60 · 2
= 216 + 120 = 336 (км) - весь путь;
2) 4 + 2 = 6 (ч.)
- общее время движения;
3) 336 : 6 = 56
(км/ч) - средняя скорость движения.
Ответ. 56
км/ч.
Можно было решить
задачу, найдя среднее арифметическое значений скоростей?
Проверим: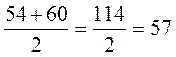 
. Видим, что получили другой ответ, следовательно,
среднее арифметическое скоростей на разных участках пути не является значением
средней скорости.
Итак, чтобы найти
значение средней скорости движения, надо значение всего пройденного пути
поделить на общее время движения.
Рассмотрим пример
2 (п. 33) по учебнику.
Комментарий к
решения. В этой задаче речь снова идет о среднее значение (цены).
Понятно, что средняя цена покупки равна стоимости покупки, разделенной на
количество единиц товара (штук, килограммов и т. д.), поэтому, чтобы найти стоимость
покупки (которая неизвестна по условию задачи), надо умножить на среднюю цену
количество килограммов (массу) всего купленного печенья.
Решение
1) 2,4 + 3,2 = 5,6
(кг) - общая масса печенья;
2) 14 · 5,6 = 78,4
(грн.) - общая стоимость покупки;
3) 10,2 · 2,4 =
24,48 (грн.) - стоит печенье первого вида;
4) 78,4 - 24,48 = 53,92
(грн.) - стоило печенье второго вида;
5) 53,92 : 3,2 =
16,85 (грн.) - цена 1 кг печенья второго вида.
Ответ. 16,85
грн.
Давайте проверим,
можно было бы получить этот ответ, использовав понятие среднего
арифметического: если х(грн.) цена печенья второго вида, то среднее арифметическое
цены:
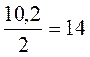, 10,2 + х = 28, х = 28 - 10,2, х = 17,8.
Видим, что эта
ответ отличается от найденной ранее. Итак, можем сделать вывод:
1. Среднее значение величины и среднее
арифметическое нескольких чисел - это разные понятия.
2. Чтобы найти среднее значение скорости
(цены), надо общий путь (общую стоимость) разделить на общее время
(количество единиц товара).
IV. Формирование умений
Ученики решают
задачи на применение понятий: средняя скорость (№№ 1001,1008), средний балл
оценок (№ 999), а также, если хватит времени, - № 1007.
V. Итог урока
Из выражений
соответствует значению средней скорости движения, если машина ехала 3 часа со
скоростью 58 км/ч и 4 ч со скоростью 62 км/ч.?
1) 
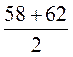; 2) 
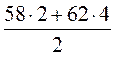; 3)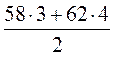 
.
VI. Домашнее задание
п. 33, №№ 1002;
1009; 1015(2); 1018(2).