Урок 111
Тема. Среднее
арифметическое. Средние величины
Цель: сформировать
умение находить среднее арифметическое и решать упражнения на применение
этого понятия.
Тип урока:
усвоение навыков и умений.
Ход урока
И. Актуализация
опорных знаний. Разминка
Устные упражнения
1. Удвойте сумму 2,4 + 19,7 + 7,3 + 4,6.
2. Найдите четверть разницы 6,2 - 3,4.
3. Найдите число, если его пятая часть
равна произведению 1,8 · 5.
4. Сравните числа:
1) 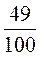 и 0,51;
и 0,51;
2) 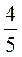 и 0,8;
и 0,8;
3) 0,4 и 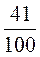 ;
;
4) 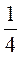 и 0,4;
и 0,4;
5) 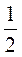 и 0,49999;
и 0,49999;
6) 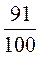 и
и 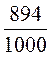 ;
;
7) 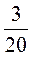 и
и 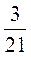 ;
;
8) 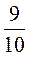 и
и 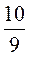 ;
;
9) 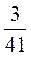 и
и 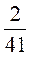 .
.
5. Решите уравнение:
1) 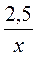 = 0,5; 2)
= 0,5; 2) 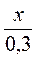 = 0,4; 3)
= 0,4; 3) 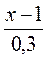 = 0,4.
= 0,4.
II. Формирование знаний
Постановка проблемы
Задача 1. В течение
июня тетка Горпина на своем огороде собрала 124 кг клубники.
Сколько килограммов
клубники собирала она ежедневно, если:
1) ежедневно урожай был одинаковым;
2) неизвестно урожай был одинаковым каждый день?
Решение
1) Понятно, что
если каждый из 31 дней июня урожай был одинаковым, то каждый день он
составляет 124 : 31 = 4 (кг).
2) В этом случае
невозможно точно ответить на вопрос, потому что возможны разные случаи. Но среднее
значение урожая 124 : 31 = 4 (кг).
Задача 2. Общий
возраст игроков футбольной команды 286 лет. Какого возраста каждый из игроков, если:
1) они ровесники;
2) неизвестно, все
они ровесники?
Решение
1) 286 : 11 = 26
(лет) - возраст каждого игрока;
2) ответить на
вопрос точно невозможно, поэтому говорят, что средний возраст игроков футбольной
команды 286 : 11 = 26 лет.
Решение
проблемы
После разбора задач
1 и 2 учитель делает выводы.
Итак, довольно часто
в повседневной жизни мы имеем дело со средними величинами (средняя
урожайность, средняя зарплата учителя, среднее количество окладов за месяц, год
и т. д.). Но как найти среднее значение величины, мы рассмотрим в следующем
урока. А вот с отдельным случаем средних величин - средним арифметическим, мы
познакомимся сегодня.
Задача 3. Туристы
за 1-ую час прошли 2,6 км. За вторую - 3,3 км, а за третью - 2,5 км. С какой
постоянной скоростью (средней скоростью) надо было им идти, чтобы пройти всего
расстояние за 3 ч.?
Решения.
Очевидно, что 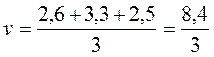 = 8,4 : 3 = 2,8 (км/ч).
= 8,4 : 3 = 2,8 (км/ч).
Итак, видим, что
для нахождения ответа задачи мы нашли сумму 3-х слагаемых и поделили ее на
3 (количество слагаемых). Следовательно, средним арифметическим нескольких чисел называют
частное от деления суммы этих чисел на количество слагаемых.
Пример 1. Найдите
среднее арифметическое чисел 23,4; 18,7; 19,6 и 20,8.
Решения.
Среднее арифметическое
равна:
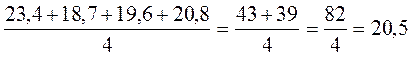 .
.
Пример 2. Среднее
арифметическое чисел 3,7 и х равен 2,15. Найдите число х.
Решение
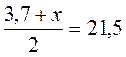 ; 3,7 + х = 21,5 · 2; 3,7 + х = 4,3; х =
4,3 - 3,7; х = 0,6.
; 3,7 + х = 21,5 · 2; 3,7 + х = 4,3; х =
4,3 - 3,7; х = 0,6.
III. Формирование умений
Ученики решают за
аналогии с примерами 1 и 2 №№ 997; 998; 1003, а также выполняют упражнения на
повторение: №№ 1015(1); 1016.
IV. Итог урока
Решая устные задания,
учащиеся повторяют основные теоретические сведения урока (определение среднего
арифметического нескольких чисел) и проверяют свои умения находить среднее
арифметическое.
Какое из чисел больше?
1) 12 или среднее арифметическое 11 и 14;
2) среднее арифметическое 7 и 8 или среднее арифметическое 10, 9
и 6;
3) среднее арифметическое 19, 11, 13 и 15 или среднее
арифметическое 12, 14, 16 и 18.
V. Домашнее задание
п. 33, №№ 1000;
1004; 1015 (2); 1018 (1).