Урок № 11
Тема. Повторение сведений о обыкновенные дроби. Основное свойство дроби
Цель: повторить сведения о обыкновенные дроби, приобретенные в 5 классе (смысл числителя и знаменателя обыкновенной дроби, запись, чтение; дробь как доля; сравнение [сложение и вычитание дробей с одинаковыми знаменателями], виды дробей: правильный и неправильный; запись неправильной дроби и смешанное число и др.); сформировать у учащихся представление о равенстве дробей (с одинаковыми знаменателями).
Тип урока: повторение и систематизация знаний.
Ход урока
И. Актуализация опорных знаний
Учитель сообщает о том, что одним из основных понятий, которые изучает математика, является понятие числа; учащиеся уже знакомы с этим понятием и знают, что числа бывают натуральными (используются для счета) и дробными (означают часть числа или сумму натурального и дробного чисел). В 5 классе они уже познакомились с разными видами дробей. Для актуализации опорных знаний учащихся предлагаются виды упражнений (на выбор учителя).
Далее учитель может предложить:
Устные упражнения
Прочитайте дроби: 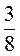 ,
, 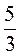 ,
, 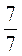 . Назовите их числитель, знаменатель и скажите, что они показывают.
. Назовите их числитель, знаменатель и скажите, что они показывают.
Сравните числитель и знаменатель каждой дроби. О чем свидетельствуют эти неровности?
Какое значение а удовлетворяет одновременно все условия: 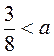 ;
; 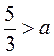 ;
; 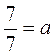 ?
?
Заполните пустые квадратики числа, чтобы равенство было верным: 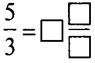 .
.
Заполните квадратики так, чтобы равенства были верными: 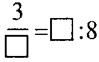 ;
; 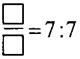 .
.
Игровой момент «Аукцион»
Учитель «выставляет» на «аукцион» три «лоты»:

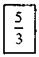
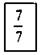
Лот № 1 Лот № 2 Лот № 3
Задача: «перебить цену» другого ученика, то есть все желающие по очереди называют, что они знают о каждое из записанных чисел. Побеждает тот ученик, который назовет последнее свойство дроби.
II. Систематизация и обобщение знаний
@ После такой активной «разминки» (см. п. 1) ученики обычно очень легко воспринимают традиционные в этой теме объяснения учителя на менее сложных или более простых примерах. Делим круг на четыре равные части, три из которых закрасим, а потом каждую четверть круга разделим еще на пять равных частей (рис. 1).
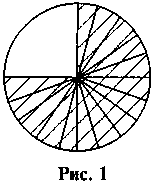
Тогда весь круг будет разделен на 4 · 5 = 20 частей, а треть всех закрашенных частей круга будет 3 · 5 таких частей. Поэтому 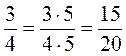 , то есть
, то есть 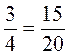 или
или 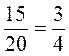 .
.
Альтернативный вариант изложения темы может быть таким.
Вспомним, что дробь - это доля отделения числителя на знаменатель, а доля не изменится при условии увеличения (или уменьшения) делимого и делителя в одну и ту же количество раз.
В любом случае ученики приходят к выводам, записанных в конспект 7.
Конспект 7 |
Основное свойство дроби |
1) 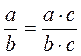 или или 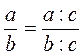 ; ;
2) равные дроби являются различными записями одного и того же числа |
Пример
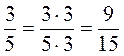 ; ;
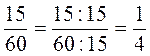 . .
|
@ Для заинтересованных учащихся можно объяснить, что и деление, и умножение числителя и знаменателя дроби на одинаковое число - равноценные действия, но в одних задачах целесообразно умножить, в других - поделить числитель и знаменатель дроби на одно и то же число. Об этом мы поговорим позже.
III. Отработка навыков
И уровень
Устные упражнения
1. Докажите равенства: 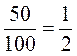 ;
; 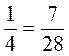 ;
; 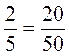 .
.
2. Верны ли равенства: 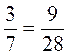 ;
; 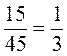 ;
; 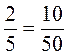 ;
; 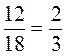 ? Ответ обоснуйте.
? Ответ обоснуйте.
3. Назовите несколько дроби, равные дроби 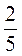 .
.
II, III уровни
Письменные упражнения
1. Умножьте числитель и знаменатель каждой дроби на 4 и запишите соответствующие равенства:  ;
; 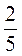 ;
; 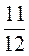 ;
; 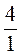 ;
; 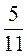 ;
; 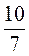 .
.
2. Разделите числитель и знаменатель каждой дроби на 5 и запишите соответствующие равенства: 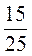 ;
; 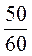 ;
; 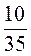 ;
; 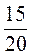 ;
; 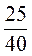 ;
; 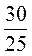 .
.
3. Запишите четыре дроби, равные дроби 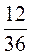 , знаменатели которых меньше знаменателя данной дроби.
, знаменатели которых меньше знаменателя данной дроби.
4. Заменит дроби 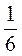 ;
; 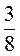 ;
; 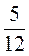 ;
; 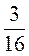 ;
; 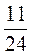 дробями со знаменателем 48.
дробями со знаменателем 48.
5. Поделите числитель и знаменатель дроби 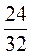 на НОД числителя и знаменателя и запишите соответствующее равенство.
на НОД числителя и знаменателя и запишите соответствующее равенство.
6. Начертите отрезок длиной 4 см. Найдите в миллиметрах 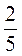 длины этого отрезка;
длины этого отрезка; 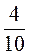 его длины. Сделайте вывод.
его длины. Сделайте вывод.
7. Изобразите на числовом луче числа:  ;
; 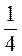 ;
; 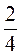 ;
; 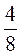 ;
; 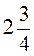 ;
; 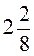 .
.
8. Сколько содержится: а) в десятых  ; б) в девятых
; б) в девятых  ; в) в двадцатых
; в) в двадцатых 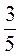 ; г) в шестых
; г) в шестых 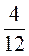 ; д) соток в
; д) соток в 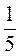 ; е) в четвертых
; е) в четвертых 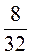 ?
?
@ Хотелось бы решить на этом уроке как можно больше упражнений, предусматривающих применение основного свойства дроби как умножение, так и деление. Поэтому можно на основе предложенных упражнений составить комплексные задачи, например такие:
1. Запишите дробь 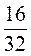 .
.
а) Умножьте его числитель и знаменатель на 7 и запишите соответствующее равенство;
б) разделите его числитель и знаменатель на 2 и запишите соответствующее равенство;
в) запишите три дроби, равные данном с меньшим знаменателем;
г) запишите три дроби, равные данном с большим знаменателем;
д) запишите дробью со знаменателем 96;
есть) поделите его числитель и знаменатель на НОД числителя и знаменателя;
ж) сколько десятых, двенадцатых содержится в дроби, что мы его получили в п.е)?
Запишите это в виде уравнений.
Замените х таким числом, чтобы было верным равенство:
а) 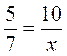 ; б)
; б) 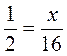 ; в)
; в) 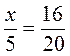 ; г)
; г) 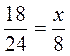 ; д)
; д) 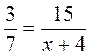 ; е)
; е) 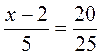 .
.
Это опорная задача, ее целесообразно разобрать отдельно после выполнения пункта ж).
Докажите, что дроби 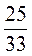 ;
; 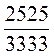 ;
; 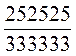 равны друг другу.
равны друг другу.
Для сильных учащихся можно предложить вспомнить признаки делимости на 101 и 10001.
IV. Итоги урока
Как формулируется основное свойство обыкновенной дроби?
Правильный запись: 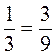 ;
; 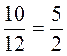 ;
; 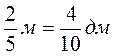 ?
?
V. Домашнее задание
1. Умножить числители и знаменатели дробей 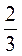 ;
; 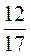 ;
; 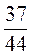 на 6, а числители и знаменатели дробей
на 6, а числители и знаменатели дробей 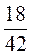 ;
; 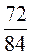 ;
; 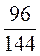 разделите на 6. Запишите соответствующие равенства.
разделите на 6. Запишите соответствующие равенства.
2. Запишите три дроби, равные дроби 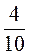 .
.
3. Замените дроби 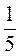 ;
; 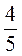 ;
; 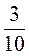 ;
; 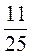 ;
;  дробями со знаменателем 50.
дробями со знаменателем 50.
4. Замените х таким числом, чтобы было верным равенство: а) 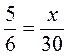 ; б)
; б) 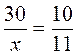 ; в)
; в) 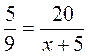 ; г)
; г) 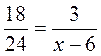 .
.
5. Выразите в копейках: 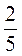 от 3 грн;
от 3 грн; 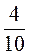 от 3 грн. Результаты сравните.
от 3 грн. Результаты сравните.
6. Найдите НОД числителя и знаменателя дроби: а) 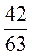 ; б)
; б) 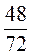 .
.
Повторите алгоритм нахождения НОД и НОК.
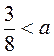 ;
; 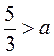 ;
; 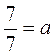 ?
? 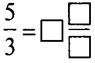
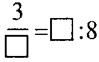 ;
; 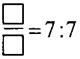 .
.
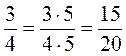 , то есть
, то есть 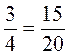 или
или 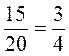 .
. 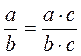 или
или 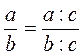 ;
;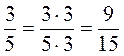 ;
;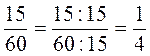 .
.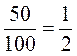 ;
; 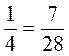 ;
; 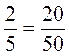 .
.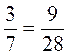 ;
; 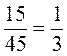 ;
; 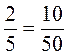 ;
; 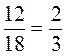 ? Ответ обоснуйте.
? Ответ обоснуйте.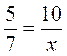 ; б)
; б) 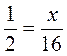 ; в)
; в) 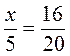 ; г)
; г) 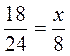 ; д)
; д) 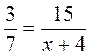 ; е)
; е) 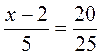 .
. 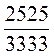 ;
; 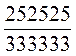 равны друг другу.
равны друг другу.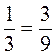 ;
; 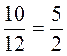 ;
; 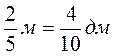 ?
?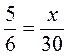 ; б)
; б) 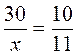 ; в)
; в) 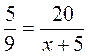 ; г)
; г) 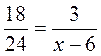 .
.