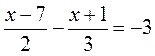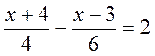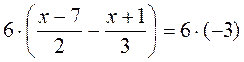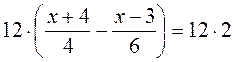Урок № 10

Тема. Решение задач с помощью линейных уравнений

Цель: систематизировать знания и умения учащихся, приобретенных во время изучения темы «Линейные уравнения с одной переменной».

Тип урока: применение знаний, умений и навыков.

Ход урока

И. Проверка домашнего задания

@ Поскольку № 1 и 2 являются задачами такого типа, которые вынесены на тематическую контрольную работу, проверке именно этих задач надо уделить больше внимания. Но одновременно надо диагностировать уровень усвоения умений предыдущих уроков. Поэтому работу на этом этапе урока можно организовать так:

Решение № 1 и 2 у доски готовят 4 ученики; фронтально проводится самостоятельная работа*, что предполагает выполнение задач именно такого типа и уровня сложности, или организуем работу в группах (предварительно проверив состояние выполнения домашнего задания, выбираем учащихся, которые справились со всем домашним заданием, и назначаем их консультантами в группах, при этом формируем группы «по интересам», то есть по такому признаку: какое задание вызвало наибольшие трудности (задачи именно с № 1 и 2), такая группа и формируется). Далее в течение 5-7 мин ученики-консультанты проводят объяснительную работу в группах, после чего кто-нибудь из учеников каждой группы (только не консультант) представляет решение задачи на доске.

(Презентация задачи означает не только воспроизведение этапов решения, но и соответствующие комментарии, базируются на теоретическом материале.)

Самостоятельная работа

Решения и ответы к самостоятельной работе

Вариант 1

1. ; НСК(2; 3) = 6; ;

 3(х - 7) - 2(х + 1) = -18; 3х - 21 - 2х - 2 = - 18; х - 23 = -18; х = -18 + 23; х = 5. Ответ. 5.

(х + 2) - 2х = 0,5; х + 2 - 2х = 0,5; - х + 2 = 0,5; х = 1,5.

Итак, в корзине было 1,5 кг винограда, а в ящике 2 · 1,5 = 3 (кг).

Ответ. 1,5 кг; 3кг.

Вариант 2

1. ; НСК(4; 6) = 12; ;

     3(х + 4) - 2(х - 3) = 24; 3х + 12 - 2х + 6 = 24; x + 18 = 24; x = 6.

Ответ. 6.

х + 12 = 1,5(х - 3); х + 12 = 1,5 х - 4,5; х - 1,5 х = -4,5 - 12; -0,5 х = -16,5;

х = -16,5 : (0,5); х = 33.

Итак, на втором участке было 33 кусты смородины, а на первом участке

33 + 9 = 42 кусты.

Ответ. 42; 33 кусты.

II. Систематизация и обобщение знаний

Контрольные вопросы к классу

1. Что называется корнем уравнения? Как проверишь, является ли число корнем уравнения?

2. Что значит решить уравнение? Сколько корней может иметь уравнение с одной переменной?

3. Два уравнения называются равносильными?

4. Какие свойства равносильных уравнений вы знаете?

5. Какое уравнение называется линейным уравнением с одной переменной?

6. В каком случае уравнение ах = b имеет один корень; не имеет корней? В любом случае любое число является корнем этого уравнения?

7. Какие этапы в решении задачи с помощью линейных уравнений вы можете выделить?

III. Применение знаний, умений и навыков

Выполнение устных упражнений (задания 1-го уровня)

1. Какое из чисел является корнем уравнения 4х + 2 = 10?
а) 1; б) -2; в) 2; г) 3?

2. Сколько корней имеет уравнение (х - 2)(х + 2) = 0?
а) Один; б) два; в) множество; г) не имеет корней.

3. Решите уравнение 3у + 5 = 7y - 3 и укажите правильный ответ:

а) -2; б) 2; в) 0,8; г) 0,5.

4. Книга и альбом стоят 6 грн., причем книга в 4 раза дороже альбома. Какое из уравнений надо составить, чтобы найти цену альбома (х - цена альбома в гривнах)?

а) х + 6х = 4; б) 6х - х = 4; в) х + 4х = 6; г) 4х - х = 6.

@ Решение устных упражнений можно организовать как самостоятельную тестовую работу.

Выполнение письменных упражнений

1. Или равносильны уравнения: 2х - 8 = 5 и х - 4 = 2,5?

2. Решите уравнение:
1) -0,75(2х + 5) + 0,25(х + 3) = 0,75;

2) ;

3) 3|2х + 1| - 7 = 2;

4) 3 - 2(1 - 2|х|) = 11 - |х|;

5)* (|x| + 2)(|х| - 3) = 0.

3. Дано уравнение (а + 3)х = 5. При котором а:

1) корнем уравнения является число -1;

2) уравнение не имеет корней;

3) корнем уравнения является любое число?

4. Решите задачу, составив уравнение:

1) По шоссе едут два автомобиля с одной и той же скоростью. Если первый увеличит свою скорость на 10 км/ч., а вторая уменьшит на 10 км/ч., то первый за 2 часа проедет столько же, сколько второй за 3 часа. С какой скоростью едут автомобили?

2) В первом бидоне в 5 раз больше молока, чем во втором. После того как из первого бидона перелили во второй 5 литров, то в первом бидоне стало в 3 раза больше молока, чем в втором. Сколько литров молока было в каждом бидоне первоначально?

3)* В двух пакетах было по 11 конфет. После того как из первого пакета взяли в 3 раза больше конфет, чем из второго, в первом пакете осталось в 4 раза меньше конфет, чем во втором. Сколько конфет взяли из каждого пакета?

IV. Итог урока

V. Домашнее задание

1. Повторить теоретический материал (см. контрольные вопросы).

2. Домашняя контрольная работа.

№ 1. Найдите корень уравнения:

1) х = 36;

2) 12х = -6;

3) 11х - 9 = 4х + 19;

4) 7х - 5(2х + 1) = 5х+15;

5) (14х + 1)(1,8 - 0,3 х) = 0.

№ 2. Решите задачу, составив уравнение.

В одном ящике было 200 кг апельсинов, а во втором - 120 кг. Из первого ящика принимали ежедневно по 30 кг, а из второго - по 25 кг. Через сколько дней в первом ящике останется в 4 раза больше апельсинов, чем во втором?

№ 3. При каком значении b имеют общие корни уравнения 2х - 9 = 3 и х + 3b = -10?