Урок 11

Тема. Решение задач

Цель урока: формирование умений учащихся применять признак параллельности и признак мимобіжності двух прямых к решению задач.

Оборудование: стереометрический набор, модель тетраэдра.

Ход урока

И. Проверка домашнего задания

1. Фронтальное опрашивание.

1) Как могут располагаться две различные прямые в пространстве?

2) Какие прямые в пространстве называются параллельными?

3) Сформулируйте признак параллельности прямых.

4) Какие прямые называются скрещивающимися?

5) Сформулируйте признак мимобіжності прямых.

2. Проверку выполнения задачи № 27 можно провести путем беседы, пользуясь рис. 36 из учебника, за такими вопросами:

1) Почему DC ║ D1C1 ?

2) На основании чего можно утверждать, что DC = D1C1 ?

3) Согласно признаку четырехугольник CDD1C1 является параллелограммом?

4) Каково взаимное расположение прямых AD1 и АВ? Почему?

5) Каково взаимное расположение прямых DC и AD1? Почему?

II. Закрепление и осмысление знаний учащихся

Решение задач

1. Точка S не лежит в плоскости треугольника АВС, точки Μ, Ν и Ρ - середины отрезков SA, SB и SC соответственно, точка Μ лежит на отрезке BN. Каково взаимное положение прямых: a) NS и АВ; б) РК и ВС; в) MN и АВ; г) МР и АС; д) KN и АС; е) KN и АС; е) MS и ВС? Ответ обоснуйте.

2. Через точку А, не лежащую на прямой а, проведены две прямые, не имеющие общих точек с прямой а. Докажите, что хотя бы одна из прямых и прямая а будут скрещивающимися прямыми.

3. Через вершину А ромба ABCD проведена прямая а, параллельная диагонали BD, а через вершину С - прямая b, не лежащая в плоскости ромба. Докажите, что: а) прямые а и CD пересекаются; б) прямые a и b - скрещивающиеся прямые.

4. Точка С делит отрезок АВ в отношении АС : СВ = m : n. Параллельные прямые, которые проходят через точки А, С, В, пересекающие некоторую плоскость в точках A1, С1, В1. Найдите отношение A1B1 : А1С1, если известно, что отрезок АВ не пересекает данной плоскости.

5. Через конец А отрезка АВ проведена плоскость α . Через конец В и точку С этого отрезка проведены параллельные прямые, которые пересекают плоскость α в точках В1 и С1. Найдите длину отрезка СС1, если: а) АС : СВ = m : n и ВВ1 = а; б) АС1 : C1Β1 = m : n и ВВ1 = b; в) АВ : ВВ1 = m : n и АС = с.

6. Через вершину D параллелограмма ABCD проведена плоскость, которая пересекает его, а через точки А, В, С - параллельные прямые, которые пересекают эту плоскость в точках А1, В1, С1 соответственно. Найдите ВВ1, если АА1 = а, СС1 = с.

7. Задача № 8* из учебника (с. 18).

8. Пусть О - точка пересечения диагоналей параллелограмма ABCD, а α - плоскость, которая пересекает параллелограмм. Через точки А, В, С, D, В проведены параллельные прямые, которые пересекают плоскость α в точках Α1, B1, C1 D1, O1 соответственно. Докажите, что:

а) АА1 + ВВ1 + СС1 + DD1 = 4 · ОО1; б) АА1 + СС1 = ВВ1 + DD1.

9. Задача № 12* из учебника (с. 19).

Решение

Точки Μ, Ν, K, L, S, Ρ - середины отрезков АВ, ВС, AC, AD, BD, CD соответственно (рис. 41). Четырехугольник MLPN - параллелограмм (поскольку MN ║ AC, MN = 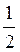AC, LP ║ AC, LP = 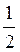AC), следовательно, ΜΡ и LN - его диагонали, которые пересекаются в точке О и делятся в этой точке пополам.

Четырехугольник LSNK - параллелограмм (поскольку LS || АВ, LS = 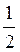АВ, NK || АВ, NK = 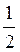АВ), следовательно, его диагонали SK и LN пересекаются в точке О и делятся в этой точке пополам. То есть, прямые, соединяющие середины отрезков АВ и CD, AC и BD, AD и ВС, пересекаются в одной точке.

III. Домашнее задание

Подготовиться к тематической аттестации и решить следующую задачу.

Дано треугольник АВС и плоскость α , которая не пересекает его. Через вершины треугольника АВС и точку Μ - середину медианы AD этого треугольника - проведены параллельные прямые, которые пересекают плоскость α в точках А1, B1, C1 и М1 соответственно. Найдите длину отрезка ММ1, если АА1 = а, BB1 = b, СС1 = с.

IV. Подведение итога урока

Вопрос к классу

1) Укажите возможные случаи расположения двух прямых в пространстве.

2) Сформулируйте признак параллельности прямых в пространстве.

3) Сформулируйте признак мимобіжності прямых в пространстве.