МАТЕМАТИКА

УРАВНЕНИЕ

Линейное уравнение с одной переменной - уравнения, сводится к каноническому виду ах + b = 0, где х - переменная, а и b - константы.

Корень уравнения ах + b = 0 определяется формулой: х = -b/а

- если а ≠ 0, множество решений L = {-b/a}.

- если а = 0, b = 0 , тогда множество корней;

- если а = 0, b ≠ 0 , тогда уравнение не имеет корней.

Линейное уравнение с двумя переменными - уравнения, сводится к каноническому виду ах + by + с = 0, где х и у - переменные, а и b - константы. Линейное уравнение с двумя переменными имеет бесконечно много решений - пар чисел (х; у), которые превращают уравнение в правильную числовое равенство. Чтобы найти его решение, надо одну из переменных заменить некоторым ее значением и решить полученное уравнение с одной переменной.

Линейное уравнение с двумя переменными - это уравнение прямой, оно определяет на координатной плоскости хОу прямая, координаты (х; у) каждой точки которого являются решением этого уравнения. Эту прямую называют графиком или геометрической моделью.

Для построения графика Л. г. с двумя переменными надо найти два его решения: (х₁;у₁) и (х₂;у₂), построить на координатной плоскости хОу точки A₁(х₁;у₁) и A₂(х₂;у₂) и провести через эти две точки прямую.

Системы уравнений

Система линейных уравнений:

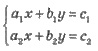
1. Имеет одно решение, если

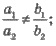
коэффициенты х и у непропорциональные; прямые пересекаются.

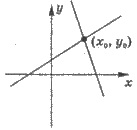
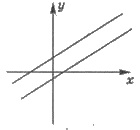
2. Не имеет решений, если

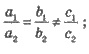
прямые параллельны.

3. Имеет множество решений, если

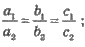
прямые совпадают.