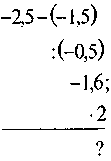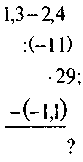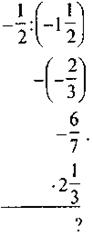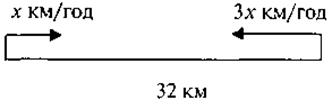
Урок № 104

Тема. Решение задач с помощью уравнений

Цель: совершенствовать умение решать задачи составлением уравнения; отработать навыки решения линейных уравнений с одним изменением и выполнения арифметических действий с рациональными числами.

Тип урока: применение знаний, умений и навыков.

Ход урока

I. Организационный момент

II. Проверка домашнего задания

@ Сплошь и рядом ученики, особенно в начале изучения темы допускают определенные ошибки при составлении таблиц, уравнений и записи пояснений к ним, поэтому на этапе проверки домашнего задания желательно, чтобы ученики имели возможность увидеть правильное решение. Учитель заранее записывает на доске решение (в виде таблиц) и уравнения. Ученики сравнивают свои записи с записями на доске и исправляют возможные ошибки. Кроме этого, можно предложить учащимся устно (по таблице) прокомментировать составление уравнения.

Также хотелось бы обратить внимание на возможные различные варианты составления уравнения (когда за неизвестное число берут не меньшую, а большую величину). Следует объяснить учащимся, что из двух вариантов составления уравнения обычно выбирают тот, в котором за х обозначено меньшую из величин.

III. Воспроизведение знаний

Устные упражнения

2. По рисунку составьте задачу, чтобы ее решение привело к уравнению 2х + 6х = 32. Решите задачу:

3. Даны 2 числа а и b. Запишите в виде равенства:

а) что сумма этих чисел 12;

б) разность этих чисел 3;

в) число а на 2 больше числа b;

г) число а на 3 меньше числа b;

д) удвоенное число а равно утроенном числу b.

IV. Совершенствование умений

@ Последний урок раздела «Решение задач с помощью уравнений» посвящен решению задач, которые условно можно назвать так: «Было, изменилось, стало».

Автор предлагает решения таких задач также начинать с составления таблицы. Обращаем внимание на то, что традиционно сложным для учащихся является понимание того, как составить равенство при условии, что одно выражение в а раз больше (меньше) другого.

Задача 1. В большом бидоне втрое больше молока, чем в малом. Когда в большой бидон долили 6 л молока, а в малый - 7 л, то в большом бидоне молока стало вдвое больше, чем в малом. Сколько молока было в каждом бидоне первоначально?

Задача 2. В одном баке 400 л бензина, а во втором - 900 л. Каждый час с первого бака выливают 20 л бензина, а из второго - 10 л. Через сколько часов в первом баке останется бензина в 4 раза меньше, чем во втором?

Задача 3. У Васи с Маричкой было поровну денег. Когда Вася купил книгу за 14 гривен, а Маша куклу за 6 гривен, то у девочки осталось денег в 3 раза больше, чем у мальчика. Сколько денег было у каждого из них сначала?

Задача 4. В одном ящике было в 7 раз больше апельсинов, чем во втором. Когда из первого ящика взяли 38 апельсинов, а из второго - 14, то во втором осталось на 87 апельсинов меньше, чем в первом. Сколько апельсинов было в каждом ящике сначала?

Дополнительная упражнение

Решите уравнение:

а) 0,3(6 - 3) = 4,5 - 0,8(у - 9);

б) .

V. Итоги урока

Какое из уравнений соответствует условию задачи: «В первой шкафу было в 4 раза меньше книг, чем во второй. Когда в первую шкаф положили 17 книг, а из второй взяли 25, то в обоих шкафах книг стало поровну. Сколько книг было в каждом шкафу сначала?»

(За х обозначим начальное количество книг в первом шкафу.)

а) х + 25 = 4х - 17; б) х + 17 = 4х - 25; в) х + 17 = х - 25; г) 4х + 17 = х - 25.

VI. Домашнее задание

1. В двух корзинах было поровну яблок. После того, как из первой корзины взяли 50 яблок, а из второго - 90, в первом яблок стало в три раза больше, чем во втором. Сколько яблок было в каждой корзине сначала?

2. В книжном шкафу было в 6 раз больше книг, чем на этажерке. После того как из шкафа взяли 46 книг, а с этажерки - 18, на этажерке осталось на 97 книг меньше, чем в шкафу. Сколько книг было первоначально в шкафу и сколько на этажерке?

3. Вычислите: .