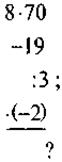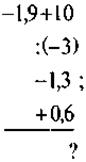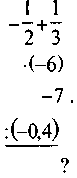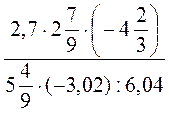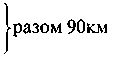Урок № 103

Тема. Решение задач с помощью уравнений

Цель: выработать у учащихся умение решать задачи на движение составлением уравнений; отработать навыки решения линейных уравнений и выполнения арифметических действий с рациональными числами.

Тип урока: применение знаний, умений и навыков.

Ход урока

I. Организационный момент

II. Проверка домашнего задания

Самостоятельная работа

Мама получила премию. На покупку пальто было потрачено всей премии, а на приобретение туфель - премии, осталось 150 гривен. Определите размер премии?

III. Отработка знаний

Устные упражнения

1. Вычислите:

2. Упростите выражение:

a) -9m + 3m; б) 0,6b - b; в) m - m; г) -2(а + 3); д) 0,5 (х - 3); е) (3х - 5).

3. Решите уравнение:

а) 3х - 2 = х + 3;

б) х - 3 = х;

в) 2(х - 3) = 4;

г) 2(х - 3) = х + 5.

4. Пусть скорость пешехода а км/ч, а велосипедиста - b км/ч. Какое расстояние будет между ними через два часа, если:

а) они вышли из пункта А одновременно в противоположных направлениях;

б) они вышли из пункта А одновременно в одном направлении;

в) они вышли одновременно из пунктов А и В навстречу друг другу, и расстояние от A до В равна 100 км?

IV. Выработка умений

@ Заметим, что шестиклассники имеют определенный опыт решения задач на движение (в 5 классе таких задач было решено немало). Сейчас мы учимся составлять уравнения по условию задачи. По мнению автора, процесс составления уравнения и запись необходимых объяснений пойдет лучше, если его сопровождать составлением и постепенным заполнением таблицы (при условии, что S = vt).

Поскольку работа с таблицей является новым элементом, желательно одну из задач решить учителю, а другие предложить ученикам.

Задача 1. Турист 3 ч ехал на велосипеде, и 2 часа шел пешком, причем пешком он шел на 6 км/ч медленнее, чем ехал на велосипеде. С какой скоростью шел турист, если всего он преодолел 38 км?

Решения. Составим таблицу и заполним ее данными в условии значениями величин

Видим, что по условию неизвестные скорости и расстояние, которое он преодолел на велосипеде и пешком. Прочитав вопрос, видим, что шуканою есть скорость движения пешком (к тому же она меньше скорости движения на велосипеде). Поэтому далее обозначаем: пусть х (км/ч) - скорость движения пешком, тогда х+6 (км/ч) - скорость движения на велосипеде, расстояние за 2 ч пешком 2х(км), а расстояние, которое преодолел турист за 3 ч на велосипеде, 3(х+6) (км). Итого за 5 ч турист преодолел 3(х+6)+2х (км), что по условию задачи составляет 38 км. Составим и решим уравнение:

3(х + 6) + 2х = 38; 3x + 18 + 2x = 38; 5x = 20; х = 20 : 5; х = 4.

Следовательно, скорость движения пешком 4 км/ч.

Ответ. 4 км/ч.

Задача 2. Автомобиль проехал некоторое расстояние за 2,5 часа. Если бы он ехал быстрее на 15 км/ч, то проехал бы ту же расстояние за 2 ч. С какой скоростью двигался автомобиль и какое расстояние он преодолел?

Задача 3. Катер прошел по течению реки расстояние от пристани А до пристани В и вернулся обратно (от В к А). Скорость течения 3 км/ч. Найдите скорость катера, если:

а) от A до В катер шел 1,5 часа, а от В до А - 2 ч; б) скорость катера против течения реки составляет 75 % от скорости катера по течению.

Дополнительная упражнение Выполните действия: .

V. Итоги урока

Составьте задачу и уравнения к ней по данным таблицы:

Решите уравнение.

VI. Домашнее задание

1. Первый поезд преодолевает расстояние между двумя городами за 2,5 ч, а второй - за 3,5 ч. Скорость первого поезда больше скорости второго поезда на 24 км/ч. Найдите скорость каждого поезда и расстояние между городами.

2. Лодка проплыл расстояние между двумя пристанями по течению реки за 0,6 ч, а на обратный путь затратил 1 час. Скорость лодки по течению реки на 6 км/ч больше скорости против течения. Найдите расстояние между пристанями.

Дополнительная упражнение

Упростите выражение-4с + 9с - с + 8 и найдите его значение при с = 0; -8; ; -0,25; -2.