Геометрическая прогрессия

Геометрической прогрессией называется последовательность отличных от 0 чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число. Это постоянное для данной последовательности число q называют знаменателем геометрической прогрессии.
Формула n-го члена геометрической прогрессии:
.
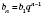
Теорема. Последовательность тогда и только тогда является геометрической прогрессией, если каждый ее член, начиная со второго, является средним геометрическим двух соседних:

. (**)
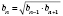
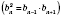
Формула суммы n первых членов геометрической прогрессии:
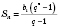
если ,
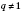
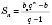
или , если , .
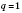
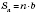
Формула суммы бесконечной геометрической прогрессии:
; .
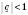
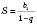
Для решения большинства задач на арифметическую и геометрическую прогрессии, а также комбинированных задач на прогрессии удобно действовать так: все данные задачи на арифметическую прогрессию выразить через a1 и d (на геометрическую - через b1 и q) и составить уравнение или систему уравнений по условию задачи (или используя свойства (*) и (**)).