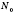
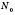
Рассмотрим какую-нибудь множество, содержащее действительных чисел, каждый элемент которой соответствует одному из натуральных чисел от 1 до , или бесконечное множество действительных чисел, каждому элементу которой можно поставить в соответствие натуральное число. Такие числа можно записать в определенном порядке. Говорят, что они образуют последовательность. Например:
2; 4; 6; 8; ... - последовательность четных чисел;
1; 3; 5; .... - последовательность нечетных чисел;
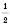
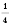
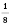
; ; ; ... - последовательность чисел вида ;
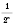
3; 6; 9; ... - последовательность чисел, кратных 3.
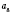
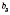
Числа, образующие последовательность, называются ее членами и обозначаются буквой с индексом. Например, - восьмой член последовательности, - третий член и т. д.
Последовательности могут быть конечные и бесконечные.
Пример конечной последовательности: 12; 14; 16; 18; 20 - последовательность четных чисел, больших 10, но не больше, чем 20. То есть:
; ; ; ; .
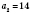
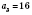
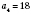
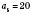
Последовательность можно задавать описанием, таблицей.
Самый удобный способ - это задать последовательность формулой n-го члена.
Например, последовательность чисел, кратных 5, можно задать формулой .
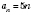
Чтобы найти, например, 20-й член последовательности, нужно вместо n подставить в формулу число 20:
.
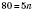
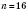
Наоборот, чтобы узнать, какой номер имеет в этой последовательности число 80, надо составить уравнение , откуда , то есть .
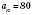
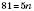
В случае уравнения делаем вывод, что числа 81 среди членов этой последовательности нет, потому что уравнение не имеет натуральных корней.
Последовательность можно также задавать формулу, выражающую любой член последовательности, начиная с некоторого, через один или несколько предыдущих.
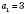
Например, пусть , тогда .
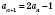
Последовательность называют возрастающей, если каждый ее член, начиная со второго, больше предыдущего. Последовательность называется убывающей, если каждый ее член, начиная со второго, меньше предыдущего.