Урок
№ 10
Тема. Смежные углы
Цель: добиться понимания
учащимися содержания следствий из теоремы о сумме смежных углов и содержания понятий
«следствие», «ссылка»; используя знания теоремы о смежных углах и ее
последствия, выработать умение решать задачи на вычисление и доказательство, в
которых говорится об смежные углы.
Тип урока: применение знаний,
умений и навыков.
Наглядность и
оборудование: таблица
«Смежные углы».
ХОД УРОКА
И. Организационный
момент
II. Проверка
домашнего задания
Математический
диктант
1. Начертите от руки
два неравные смежные углы, чтобы их общая сторона была размещена горизонтально.
2. Начертите два
смежные углы так, чтобы их стороны, которые доповняльними півпрямими, были
размещены вертикально.
3. Начертите два
несмежные углы, чтобы они имели одну общую сторону и оба были тупыми.
4. Начертите два
несмежные углы, одна пара сторон которых является доповняльними півпрямими.
5. Постройте угол AOB,
что равен 70°. Начертите два угла, каждый из которых является смежным с данным углом.
Найдите градусные меры этих углов.
Правильность
выполнение работы обязательно проверяем. Это можно сделать с помощью
заранее заготовленных записей за доской или на пленке кодоскопа.
III. Формулировка
цели и задач урока
Основная цель урока
формулируется как необходимость ознакомления с соотношениями, правильными для
смежных углов, основанные на теореме о сумме смежных углов.
IV.
Актуализация опорных знаний
Выполнение
устных упражнений
1. Какое из чисел 30°,
130°, 89°, 90°,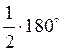 
является
градусной мерой углов:
а) тупой;
б) острого;
в) прямого?
2. Сколько градусов
может составлять сумма:
а) двух прямых
углов;
б) двух острых
углов;
в) двух тупых
углов;
г) тупого и прямого
углов;
д) прямого и
острого углов?
V. Усвоение новых
знаний
План изучения
нового материала
1°. Формулировка и
доведение последствий.
2°. Представление о
содержание понятий: «следствие», «ссылки».
3°. Пример задачи
(следствие 4).
Методический комментарий
В зависимости от уровня
подготовки учащихся, изложение новых понятий урока может осуществлять учитель или
учащиеся работают с учебником самостоятельно.
Также можно
организовать практическую работу в группах, что приведет к «открытию» учащимися
сформулированных и доказанных в учебнике следствий из теоремы о сумме смежных
углов.
VI. Первичное
осознание нового материала
Выполнение
устных упражнений (по готовым рисункам)
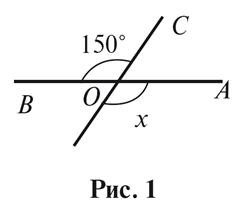
1. Найдите угол x (рис.
1)
2.
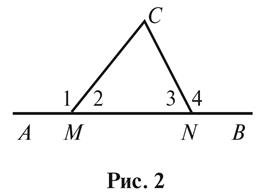
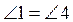. Докажите, что 
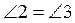(рис. 2).
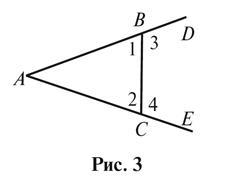
3. 
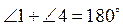(рис. 3).
Докажите, что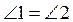 
;
.
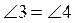Выполнение
письменных упражнений
1. Углы 1 и 2, а также
углы 3 и 4 - две пары смежных углов. Сравните углы 2 и 4, если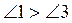 
.
2. Найдите данный угол,
если сумма двух смежных с ним углов равна 240°.
3. Биссектриса угла
образует с лучом, доповняльним в стороны данного угла, угол 130°. Найдите
данный угол.
4 (дополнительная).
Разность двух смежных углов относится к одному из них как 5 : 2. Найдите эти
смежные углы.
Во время
решения задач 1 и 2 желательно требовать от учеников ссылку не на теорему
о сумме смежных углов, а соответствующее следствие.
VII. Итоги урока
Вместо... поставьте
такое слово, чтобы утверждение было верным:
1) Угол, смежный с
прямым углом...
2) Угол, смежный с
острым углом...
3) Угол, смежный с
тупым углом...
4) Если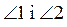 
- смежные, 
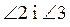- смежные, то 
...
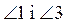5) Если 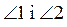- смежные, 
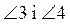- смежные и , 
.
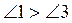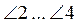VIII. Домашнее
задача
Устно выполнить
упражнения.
1. Рисунок, на котором
изображены смежные углы, перегнули по прямой, содержит их общую сторону.
При этом другие стороны данных углов совпали. Найдите данные смежные углы.
2. Найдите угол,
смежный с углом, который равен 30°; 60°; 90°; 135°.
Письменно
решить задачи.
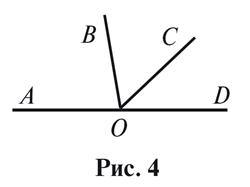
1. Найдите угол BOC (рис.
4), если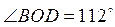 
,
.
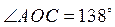2. Найдите угол,
сторона которого образует с лучом, доповняльним до биссектрисы данного угла, угол
165°.
3. Углы (mn) и (kp) есть
смежными с углом (np). Среди лучей m, n, k, p назовите пары доповняльних лучей.
4. Углы (ab) и (bc)
смежные. Углы (bc) и (cd) также смежные, причем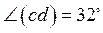 
. Найдите углы (ad) и (ab).
Источники:
1. Уроки геометрии. 7 класс./ С. П. Бабенко
- Х.: Изд. группа «Основа», 2007.- 208 с.