Урок № 9

Тема. Смежные углы

Цель: добиться сознательного понимание учащимися содержания понятия «смежные углы» и теоремы о сумме смежных углов.

Сформировать у учащихся умения:

· строить угол, смежный с данным;

· находить смежные углы на рисунке;

· используя содержание теоремы о сумме смежных углов, решать задачи базового и продвинутого уровней на вычисление градусных мер смежных углов; осуществить диагностику усвоения учащимися знаний об аксиоме измерения углов и свойства параллельных прямых и умение применить эти утверждения для решения задач.

Тип урока: усвоение знаний, умений и навыков.

Наглядность и оборудование: таблица «Смежные углы»; набор демонстрационного чертежных принадлежностей.

ХОД УРОКА

И. Организационный момент

II. Проверка домашнего задания

Самостоятельная работа

Вариант 1

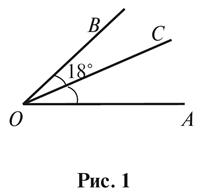
1. Дано:OC - биссектриса угла AOB. Найдите угол AOB (рис. 1).

2. Могут ли два прямые, имеющие общую точку, быть параллельны третьей прямой?

3. Луч c - биссектриса угла (bd), а луч a - биссектриса угла (bc). Найдите угол (bd), если угол (ad) равен 96°.

Вариант 2

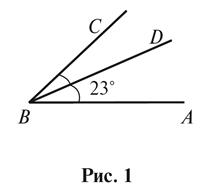
1. Дано: BD - биссектриса угла ABC. Найдите угол ABC (рис. 1).

2. Могут ли два прямые, параллельные третьей, иметь общую точку?

3. Луч a - биссектриса угла (bc), а луч d - биссектриса угла (ac). Найдите угол (ac), если угол (bd) равен 105°

После выполнения самостоятельной работы обязательно провести проверку.

III. Мотивация учебной деятельности учащихся

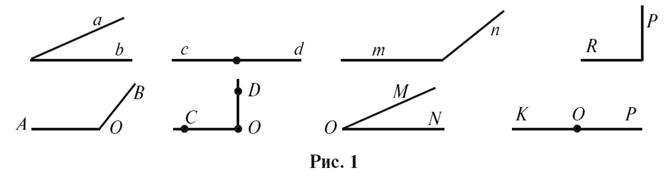
Задача 1. Углы, изображенные на рисунке 1, разделите на группы по их градусной мере. Которые группы вы образовали?

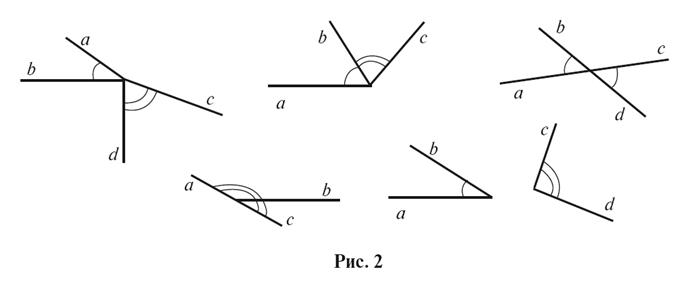
Задача 2. Опишите словами, используя названия элементов углов, особенности взаимного расположение углов (рис. 2). Какой из случаев лишний? Сделайте вывод.

IV. Формулировка цели и задач урока

Исходя из соображений, что получили на предыдущем этапе урока, учитель формулирует цель - изучение одного из случаев взаимного расположения двух углов на плоскости, и выдвигает задачи:

· дать определение такого вида расположение и научиться это определение использовать для построения и распознавание углов такого вида;

· сформулировать и доказать теорему, которая бы выражала свойство углов такого вида.

V. Актуализация опорных знаний

Выполнение устных упражнений

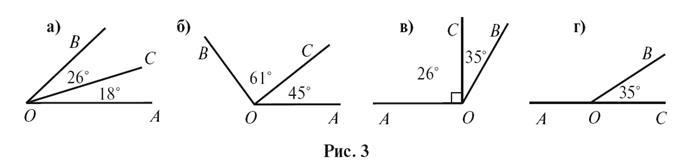
Найдите угол AOB на рисунке 3.

VI. Усвоение новых знаний

План изучения нового материала

1°. Представление о смежные углы. Определение.

2°. Теорема о сумме смежных углов и ее доведения.

Методический комментарий

Определение смежных углов и формулировки и доказательства теоремы о сумме смежных углов в новом учебнике полностью совпадает с аналогичными утверждениями, которые подаются в учебнике О. В. Погорелова (Геометрия. 7-9). Но введение самого определения смежных углов авторы учебника осуществили другим способом, акцентируя на взаимном расположении сторон смежных углов.

Также важно обратить внимание учащихся на необходимость точного воспроизведения определение смежных углов. Чтобы убедить учеников в этом, можно после введения обозначения предложить им работу по готовым чертежам.

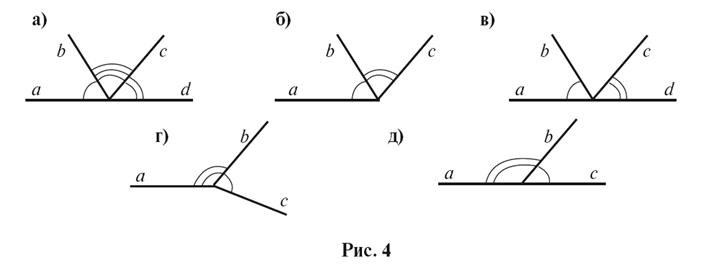
Или являются смежными углы, изображенные на рисунке 4? Почему?

После работы с определением смежных углов, желательно разобрать с учащимися процесс построения угла, смежного с данным. Поскольку теорема о сумме смежных углов является достаточно простой и доведение ее опирается на аксиому измерения углов, можно предложить учащимся проработать ее самостоятельно.

Важно также предупредить традиционную ошибку учащихся: утверждение, обратное к названной теоремы, не является правильным (осознать логическую связь: смежные углы сумма 180°, только в таком порядке).

После изложения нового материала обратиться к обобщенной таблицы «Смежные углы».

Таблица

VII. Первичное осознание нового материала

Выполнение устных упражнений

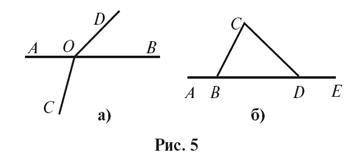
1. Есть ли на рисунке 5 пары смежных углов?

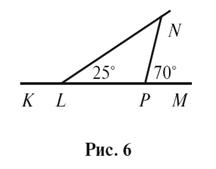
2. Найдите градусные меры углов KLN и LPN на рисунке 6.

Выполнение графических упражнений

Начертите развернутый угол (ab).

а) Из вершины этого угла проведите луч c так, чтобы угол (ac) был тупым. Назовите образованы смежные углы.

б) Измерьте транспортиром угол (cb) и вычислите градусную меру угла (ac), пользуясь теореме о смежных углах.

в) Проведите луч d, делящей угол (ac) на два угла. Сколько пар смежных углов образовалось на рисунке?

Выполнение письменных упражнений

1. Найдите смежные углы, если:

а) их градусные меры относятся как 5 : 31;

б) их разность равен 70°.

2. Две прямые пересекаются. Сколько пар смежных углов при этом образовалось?

3. Биссектриса делит угол AOB на два угла, один из которых равен 50°.

Найдите градусную меру угла, смежного с углом AOB.

4 (дополнительная). Или правильно, что два угла, которые имеют общую сторону и имеют сумму 180°, является смежными?

VIII. Итоги урока

Вопрос к классу

1. Два угла имеют общую сторону. Означает ли это, что:

а) эти углы имеют общую вершину;

б) эти углы имеют две другие стороны - доповняльні півпрямі;

в) эти углы есть смежными;

г) их сумма равна 180°?

2. Один из смежных углов равен α. Чему равен другой угол?

IX. Домашнее задача

Изучить теорему о сумму смежных углов; повторить виды углов по их градусной мере.

Устно выполнить упражнения.

1. Два угла имеют общую сторону. Означает ли это, что:

а) данные углы имеют общую вершину;

б) сумма этих углов равна 180°?

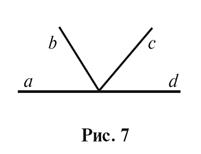
2. Лучи b и c делят развернутый угол (ad) на три угла (рис. 7). Сколько пар смежных углов при этом образуется? Назовите эти углы.

3. Найдите угол, смежный с углом, который равен: 30°; 60°; 90°; 135°.

Письменно решить задачи.

1. Найдите смежные углы, если один из них:

а) в три раза больше, чем второй;

б) на 20° меньше, чем второй.

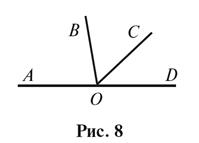
2. На рисунке 8 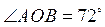, 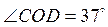. Найдите угол BOC.

Источники:

1. Уроки геометрии. 7 класс./ С. П. Бабенко - Х.: Изд. группа «Основа», 2007.- 208 с.