Определение. Аксиомы

Геометрия - это наука о свойствах геометрических фигур.
Обратите внимание: геометрическая фигура - это не только треугольник, круг, пирамида и т.д., но и любое множество точек.
Планиметрия - это раздел геометрии, в котором изучаются фигуры на плоскости.
Точка и прямая являются основными понятиями планиметрии. Это означает, что этим понятием нельзя дать точное определение. Их можно только представить, опираясь на опыт и перечислив их свойства.
Утверждения, справедливость которых принимается без доказательства, называются аксиомами. Они содержат формулировки основных свойств простейших фигур.
Утверждения, которые доказывают, называются теоремами.
Определение - это объяснение какого-либо понятия, которое опирается или основные понятия, или понятия, которые определены ранее.
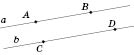
Обозначения: точки обозначаются большими латинскими буквами; прямые - строчными латинскими буквами или двумя большими латинскими буквами (если на прямой обозначены две точки).
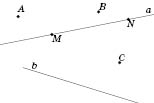
На рисунке точки A, B, C, N, М и прямые a и b. Прямую а можно обозначить как прямую MN (или NM).

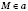
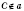
Запись означает, что точка M лежит на прямой а. Запись означает, что точка С не лежит на прямой а.
Надо понимать, что прямые a и b на рисунке пересекаются, хотя мы не видим, в точке.

Основные свойства (аксиомы) принадлежности точек и прямых на плоскости

Аксиома И.
1. Какова бы не была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
2. Через любые две точки можно провести прямую, и только одну. (Надо понимать, что здесь содержатся два утверждения: во-первых - существование такой прямой, а во-вторых - ее единственность.)
Аксиома II. Из трех точек на прямой одна и только одна лежит между двумя другими.
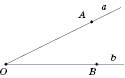
Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными ее точками. Эти точки называются концами отрезка. На рисунке изображен отрезок АВ (отрезок обозначают, записывая его конце).

Основные свойства (аксиомы) измерение отрезков

Аксиома III.
1. Каждый отрезок имеет определенную длину, большую нуля.
2. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

Основное свойство размещения точек относительно прямой на плоскости

Аксиома IV. Прямая разбивает плоскость на две полуплоскости.
Это разбиение имеет такое свойство: если концы какого-нибудь отрезка принадлежат одной півплощині, то отрезок не пересекает прямую; если концы отрезка принадлежат разным півплощинам, то отрезок пересекает прямую.
Півпрямою, или лучом,называют часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной на ней точки. Эта точка называется начальной точкой луча. Различные півпрямі одной прямой с общей начальной точкой называются доповняльними.
На рисунке представлены лучи AB (он же AC), DA (или DB, DC), BC, CB (или CA, CD), BA (или BD), AD.

Лучи AB и AD, BC и BD - доповняльні. Лучи BD и AC не является доповняльними, потому что у них разные отправные точки.
Угол - это фигура, которая состоит из точки - вершины угла - и двух различных півпрямих, выходящих из этой точки,- сторон угла.
Угол, представленный на рисунке, можно обозначить так: , , .

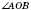
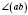
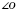
Если стороны угла являются доповняльними півпрямими, угол называют развернутым:

Говорят, что луч проходит между сторонами угла, если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на его сторонах. Для развернутого угла считаем, что любой луч, который исходит из его вершины и отличный от его сторон, проходит между сторонами угла.

Основные свойства измерения углов

Аксиома V.
1. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен .
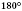
2. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

Основные свойства откладывания отрезков и углов

Аксиома VI. На любой півпрямій от ее начальной точки можно отложить отрезок данной длины, и только один.
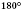
Аксиома VII. От любой півпрямої в данную півплощину можно отложить угол с данной градусной мере, меньше , и только один.
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки - его сторонами.
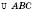
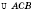
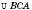
Треугольник на рисунке можно обозначить так: или , и т. д.

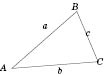
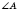
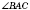
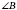
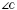
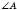
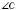
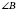
Основные элементы предоставления выше треугольника: стороны AB, AC, BC (или a, b, c); углы (или ), , . и - прилегающие к стороне AC. - противоположный стороне AC.
Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны. При этом соответствующие углы должны лежать против соответствующих сторон.
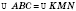
Запись означает (см. рисунок), что:
; ;
; ;
; .

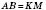
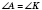
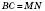
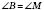
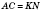
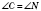
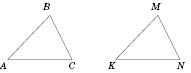
Основное свойство существования равных треугольников

Аксиома VIII. Каков бы ни был треугольник, существует треугольник, равный ему в заданном размещении относительно данной півпрямої.
Прямые называются параллельными, если они не пересекаются.
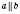
Параллельные прямые, изображенные на рисунке, можно обозначить так: или .

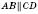
Аксиома параллельных прямых

Аксиома IX. Через точку, не лежащую на данной прямой, можно провести на плоскости не более чем одну прямую, параллельную данной.
Обратите внимание: аксиома утверждает единственность такой прямой, но не утверждает его существование.

Взаимное расположение прямых на плоскости

Две прямые на плоскости могут:
• совпадать;
• быть параллельными (т.е. не пересекаться);
• иметь одну общую точку.
(Действительно, если бы две прямые могли иметь хотя бы две общие точки, то через эти две точки проходили бы две различные прямые, что противоречит аксиоме И, п. 2).

Содержание

Вперед