АЛГЕБРА И НАЧАЛА АНАЛИЗА
Раздел И. ЧИСЛА И ВЫРАЖЕНИЯ
§27. СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
3. Знаки тригонометрических функций по четвертям.
Синус угла а является ординатой точки Гα(х;у) единичного круга (рис. 19). В i И II четвертях в > 0, а в
III и IV четвертях в 0. Поэтому sin
α > 0, если α - угол i или II четверти, и sin α 0, если α - угол III или IV четверти.
Косинус угла α является абсциссой точки Гα(х;у) единичного круга (рис. 19). В i И IV четвертях х > 0, а в
II и III четвертях х 0. Поэтому cos
α > 0, если α - угол И или IV четверти и cos α 0, если α - угол II или III четверти.
Так 
то
tgα и ctg α зависят от знаков sin α и cos
α. В i И III четвертях sin α и cos
α имеют одинаковые знаки, а во II и IV
четвертях разные. Поэтому tg
α > 0 и ctg α > 0, если α - угол i или III четверти, и tg α 0 и ctg
α 0, если α - угол II или IV четверти.
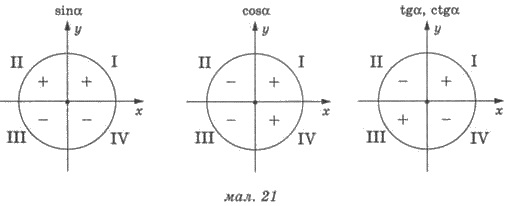
Знаки тригонометрических функций в
каждой из четвертей представлены на рисунке 21.
Пример. Сравнить с нулем: 1) соs152°; 2) tg3 ∙ sиn4 .
Решения. 1) Поскольку 152° - угол
II четверти, то соs152° 0 .
2) 3 радианы ≈ 3 ∙
57° = 171°, поэтому 3 радианы - угол II четверти и tg3 0 .
4 радианы ≈ 4 ∙
57° = 228°, поэтому 4 радианы - угол III четверти и sиn4 0. Окончательно имеем tg3 ∙
sиn4 > 0 .