Свойства функций
Функция называется
возрастающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Функция называется
убывающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Если функция возрастает (убывает) на всей области определения, ее называют возрастающей (убывающей).
Примеры
1. Линейная функция
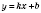
.
При
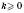
функция возрастающая (рисунок слева), при
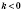
- нисходящая (рисунок справа).
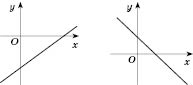
Чтобы лучше это понять, возьмите
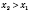
и проследите, какие значения
у соответствуют
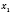
и
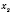
.
2. Функция
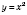
.
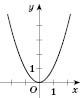
При
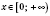
функция возрастающая (см. рисунок).
При
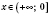
функция убывающая.
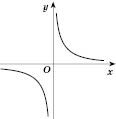
3. Обратная пропорциональность
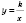
.
Если
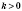
, то функция убывающая при
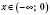
и при
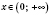
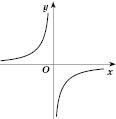
(рисунок 1); если
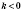
- возрастающая функция при
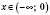
и при
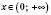
(рисунок 2).
Обратите внимание, что нельзя говорить об этих функциях, что они растут или падают на всей области определения.
Действительно, рассмотрим функцию
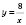
.
Пусть
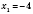
,
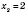
;
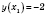
;
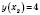
;
Следовательно,
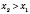
, а
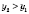
, хотя по определению убывающей функции должно выполняться условие
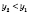
.
Функция называется
парной, если:
1) область ее определения симметрична относительно 0, т.е.
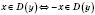
;
2)
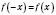
.
Противоположным значениям аргумента соответствует одно и то же значение функции.
График четной функции является симметричным относительно оси
y.
Примеры четных функций
1.
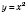
;
1)
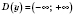
- симметричная относительно 0.
2)
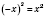
. Функция парная.
2.
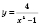
;
1)
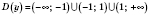
- симметричная относительно 0.
2)
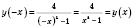
.
Функция парная.
Функция называется
нечетной, если:
1) область ее определения симметрична относительно 0;
2)
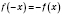
.
Противоположным значениям аргумента соответствуют противоположные значения функции.
График нечетной функции является симметричным относительно начала координат.
Примеры нечетных функций
1.
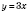
;
1)
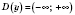
- симметричная относительно 0.
2)
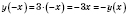
. Функция нечетная.
2.
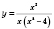
.
Чтобы найти
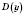
, решим уравнение
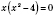
.
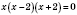
;
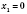
;
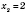
;
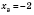
.
Итак, в
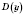
входят все действительные числа, кроме чисел 0; 2; -2.
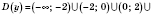
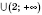
- симметрична относительно 0.
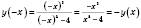
. Функция нечетная.
Обратите внимание: функция может быть ни четным, ни нечетным.