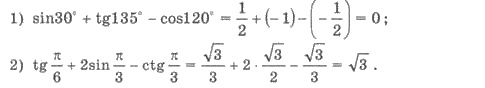АЛГЕБРА И НАЧАЛА АНАЛИЗА
Раздел И. ЧИСЛА И ВЫРАЖЕНИЯ
§26. ОПРЕДЕЛЕНИЕ СИНУСА, КОСИНУСА, ТАНГЕНСА И КОТАНГЕНСА ЧИСЛОВОГО АРГУМЕНТА.
5. Тригонометрических функций некоторых углов.
Исходя из введенных в предыдущем
пункте определений, найдем тригонометрические функции углов 0°; 90°; 180°; 270°;
360°.
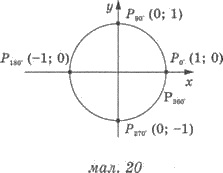
Точка Г0° (рис. 20) имеет координаты (1;0). Поэтому sиn0° = 0 ; соs00 = 1; tg0° = 0; сtg0° - не существует.
Точка Р90° (рис. 20) имеет координаты (0;1).
Поэтому sиn90° = 1; соs90°
= 0 ; tg90° - не существует; сtg90° = 0.
Точка Р180° (рис. 20) имеет координаты (-1;0). Поэтому
sиn1800 = 0; соs180° = -1; tg180°
= 0 ; - не существует.
Точка Р270° (рис. 20) имеет координаты (0;-1).
Поэтому sиn270° = -1; соs270°
= 0 ; tg270° - не существует; ctg270° = 0.
Точка Р360° (рис. 20) имеет такие же координаты, как и точка Г0°.
Следовательно, sin360° = sиn0° = 0; соs360° = соs0° = 1; tg360° = tg0° = 0; ctg360° -
не существует.
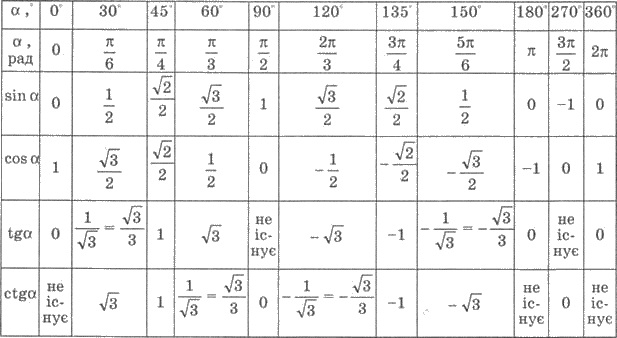
Обобщим полученные данные, а также
данные об синус, косинус, тангенс и котангенс углов 30°; 45°; 60°; 120°; 135°;
150° к таблице.
Для удобства пользования представлен как
градусную меру угла α, так и радіанну.
Пример.