АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел И. ЧИСЛА И ВЫРАЖЕНИЯ

§26. ОПРЕДЕЛЕНИЕ СИНУСА, КОСИНУСА, ТАНГЕНСА И КОТАНГЕНСА ЧИСЛОВОГО АРГУМЕНТА.

3. Угол произвольной величины.

Рассмотрим единичный круг. Радиус ОА, где А(1;0) назовем начальным радиусом (рис. 10).

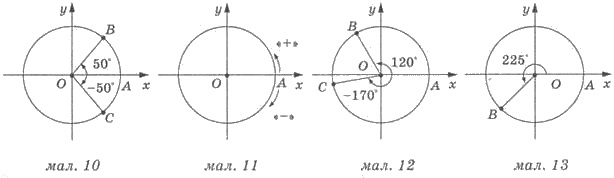
Повернем радиус ОА вокруг точки О на 50° против часовой стрелки. Тогда радиус ОА займет положение ОВ. Говорят, что угол поворота равен 50°. Вернем теперь начальный радиус ОА на угол 50° по ходу часовой стрелки; получим радиус ОС. В этом случае говорят, что угол поворота равен -50°. На рисунке 10 стрелками показано углы поворота 50° и -50°. Вообще, при повороте начального радиуса против часовой стрелки, угол поворота считается положительным, а по ходу часовой стрелки - отрицательным (рис. 11).

Угол поворота может быть любым действительным числом. На рисунке 12 показаны углы поворота 120° и 170°.

Чтобы обозначить угол поворота 225°, сначала вернем начальный радиус ОА на 180° против часовой стрелки, а потом еще на 45° в том же направлении (180° + 45° = =225°). На рисунке 13 стрелке показано угол поворота 225°.

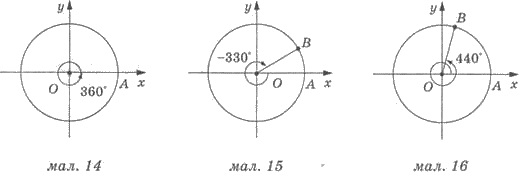
Если начальный радиус сделает полный оборот против часовой стрелки, то угол поворота будет равен 360° (рис. 14).

На рисунке 15 показано угол поворота -330°, а на рисунке 16 - угол поворота 440°.

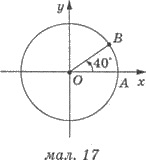
Пусть при повороте на угол 40° начальный радиус ОА перешел в радиус ОВ (рис. 17). Если после этого радиус ОВ повернуть на угол 360° или -360°, то снова получим радиус ОВ. Таким образом сделаем вывод о том, что радиус ОА переходит в радиус ОВ и при повороте на углы 40° + 360° = 400° и 40° - 360° = -320° да и вообще при повороте на угол 40° + +360°k, где k - любое целое число (k 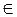Z).

С другой стороны, любой угол а можно представить в виде α = α₀ + 360°k, где 0 ≤ α₀ 360°, k - целое число.

Например: 1100° = 20° + 360° ∙ 3 ; - 640° = 80° + 360° ∙ (-2).

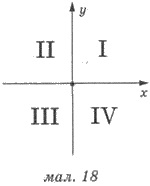
Из геометрии известно, что координатные оси делят координатную плоскость на четыре четверти (рис. 18). Если при повороте на угол а начальный радиус ОА перешел в радиус ОВ, то в зависимости от того, в какой координатной четверти будет этот радиус, угол а называют углом этой четверти.

Пример. Углом которой четверти есть угол:

1) α = 1999°; 2) β = -2010°.

Решения. 1) Поскольку α = 1999° = 199° + 360° ∙ 5, то α = 1999° - угол III четверти.

2) Поскольку (3 = -2010° = 150° + 360° ( -), то р = -2010° - угол II четверти.