Примеры функций и их графиков

Линейная функция

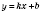
Линейной называется функция, которую можно задать формулой , где х - аргумент, а k и b - данные числа.
График линейной функции - прямая. k называется угловым коэффициентом прямой, которая является графиком линейной функции. Каждая прямая на координатной плоскости, которая является перпендикулярной к оси абсцисс,- график некоторой линейной функции.
Через две точки можно провести одну и только одну прямую, поэтому для построения графика линейной функции достаточно знать координаты двух точек (очень хорошо, если это будут точки пересечения графика с осями). Точка пересечения графика с осью абсцисс имеет ординату 0, а точка пересечения графика с осью ординат имеет абсцису 0.
Пример
Постройте график функции .
, ; , , , .

x	0	1,5
y	-3	0

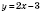
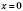
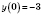
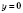
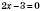
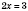
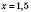
Построим график (см. рисунок).

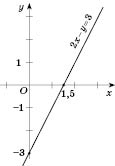
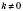
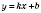
Если в линейной функции , то график функции пересекает ось абсцисс;
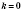
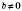
если , то график функции - прямая, параллельная оси абсцисс;
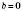
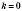
если , , график функции совпадает с осью абсцисс.
Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.
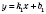
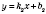
Можно найти координаты точки пересечения прямых, не выполняя построения графиков функций. Так, если прямые заданы уравнениями и , то достаточно решить систему уравнений:

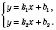
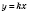
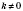
Линейную функцию, которая задается формулой , где , называют прямой пропорциональностью.
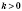
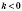
График прямой пропорциональности - прямая, проходящая через начало координат. Если , график лежит в I и III координатных четвертях, а если - то во II и IV координатных четвертях.
Примеры
1) , , .
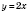
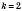
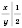
2) , , .
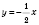
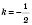
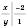
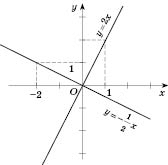
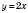
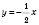
Построим в одной системе координат графики функций и (см. рисунок).

Обратная пропорциональность

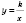
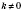
Функцию, заданную формулой , где х - независимая переменная, - данное число, называют обратной пропорциональностью.
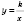
Область определения функции - множество всех чисел, кроме 0.
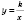
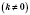
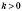
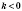
График функции - гипербола, симметричная относительно начала координат. Когда , ветки такой гиперболы расположены в I и III координатных углах, когда - в II и IV.
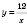
В качестве примера построим график функции . Заполним таблицу (значение x задаем, y - вычисляем по формуле :

x
y

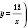
Нанесем полученные точки на координатную плоскость. Соединив эти точки плавной линией, получим график (см. рисунок):

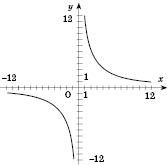
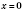
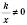
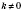
Обратите внимание на поведение графика вблизи осей координат. График до них бесконечно приближается, но не пересекает. Действительно, не входит в область определения, следовательно, точки пересечения с осью Oy нет. ни при каком значении х, значит, если , точки пересечения с осью Ox нет.

Функция

Заполним таблицу (значение x задаем, y - вычисляем по формуле y = x2).

x	0
y	0	1	4	9	0,25

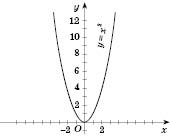
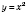
Нанесем найденные точки на координатную плоскость. Соединив эти точки, получим график функции (см. рисунок ниже).
Область определения этой функции - множество всех действительных чисел.
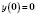
. График проходит через начало координат .
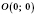
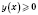
при всех значениях х. Все точки графика расположены ниже оси Ох.
Противоположным значениям аргумента соответствуют равные значения функции, то есть график симметричен относительно оси ординат.

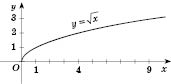
Функция

Область определения - множество всех неотрицательных действительных чисел.
График - одна ветвь параболы, которая расположена в I координатном углу (см. рисунок).

Назад

Содержание

Вперед